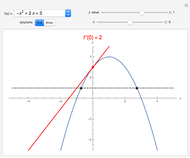
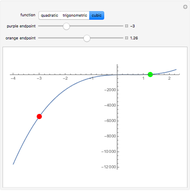
Extreme Value Theorem
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
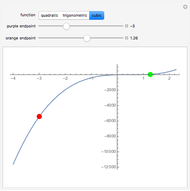
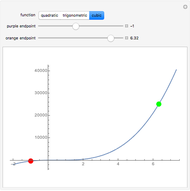
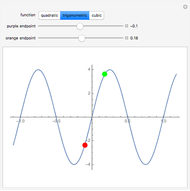
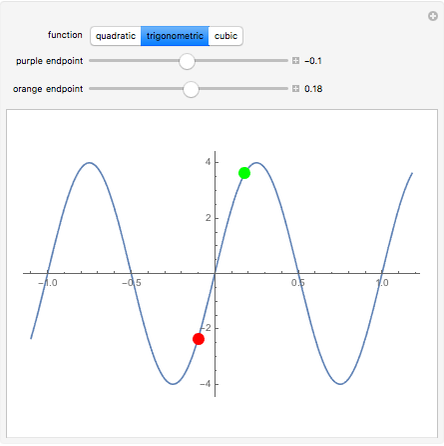
If the function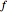 
is continuous over the closed interval 
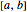, then there is at least one maximum value (green) and one minimum value (red) of 
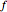in that interval.
Contributed by: Jacqueline Wandzura (March 2011)
Additional contributions by: Stephen Wandzura
Open content licensed under CC BY-NC-SA
Snapshots
Details
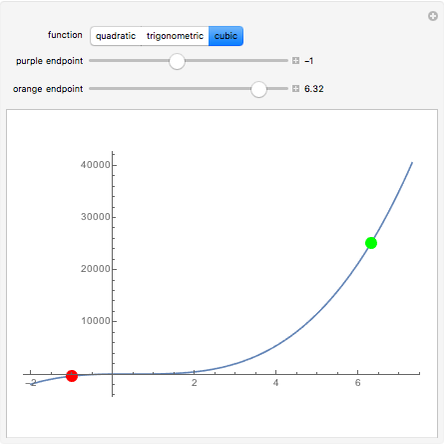
Snapshot 3: If a function is monotone increasing or decreasing in a given interval, then the endpoints must be the extrema.
Permanent Citation
"Extreme Value Theorem"
http://demonstrations.wolfram.com/ExtremeValueTheorem/
Wolfram Demonstrations Project
Published: March 7 2011
Fundamental Theorem of Calculus
Stephen Wilkerson and LTC Hartley
Mean Value Theorem
Michael Trott
Cauchy Mean-Value Theorem
Soledad Mª Sáez Martínez and Félix Martínez de la Rosa
Integral Mean Value Theorem
Chris Boucher
A Generalization of the Mean Value Theorem
Soledad Mª Sáez Martínez and Félix Martínez de la Rosa
Two Integral Mean Value Theorems
Soledad María Sáez Martínez and Félix Martínez de la Rosa
Fundamental Theorem of Calculus and Initial Value Problems
Raquel Ruiz de Eguino
Two Integral Mean Value Theorems of Flett Type
Soledad María Sáez Martínez and Félix Martínez de la Rosa
Flett's Theorem
Soledad Mª Sáez Martínez and Félix Martínez de la Rosa
Rolle's Theorem
Laura R. Lynch
