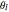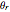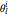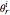Eye Parameters (Visual Depth Perception 6)

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
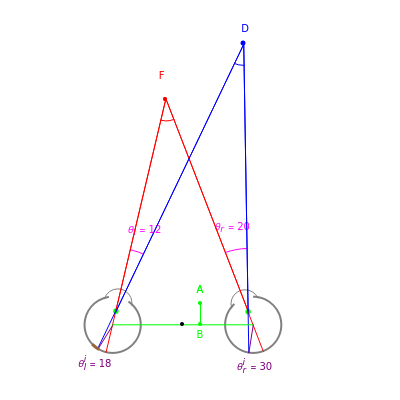
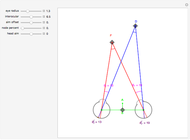
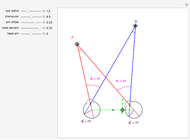
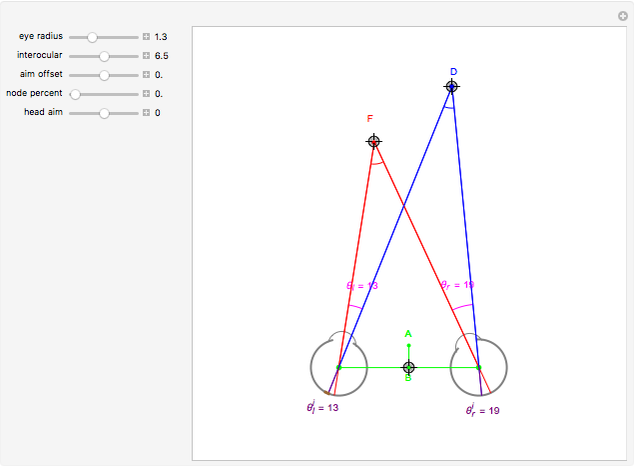
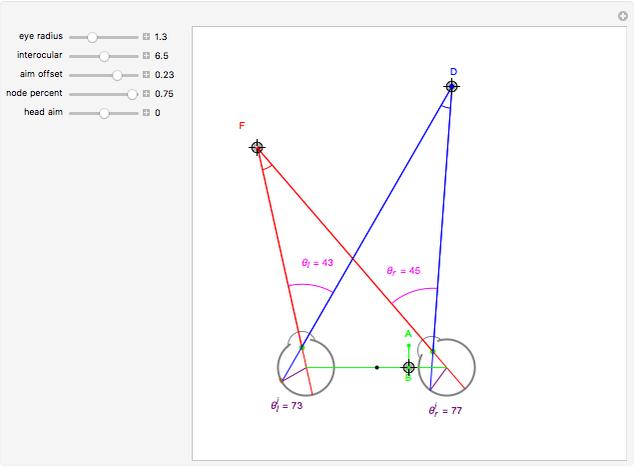
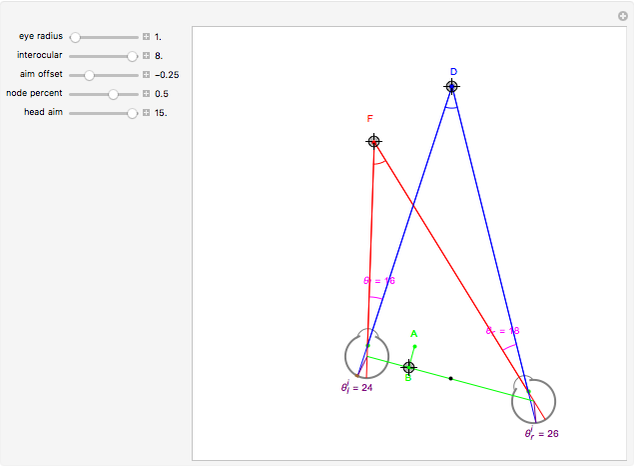
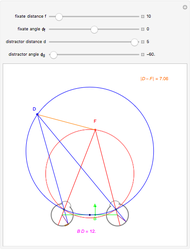
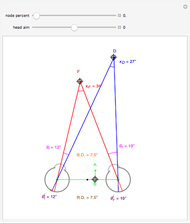
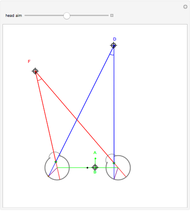
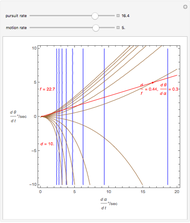
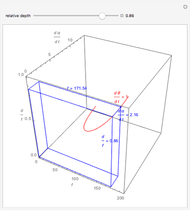
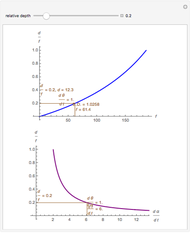
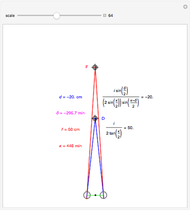
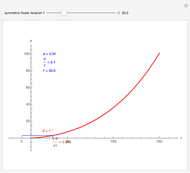
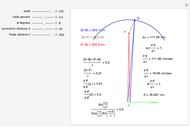
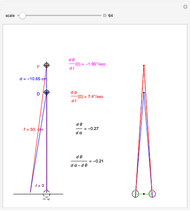
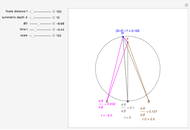
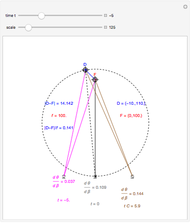
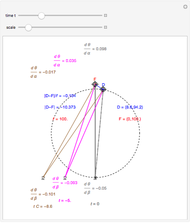
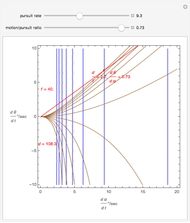
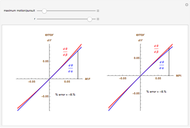
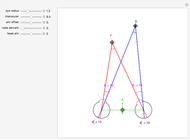
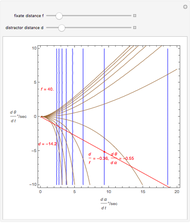
This Demonstration allows you to manipulate several eye parameters: eye radius, interocular distance, and offset in a model of the horizontal fixation plane of the eyes "fixed" on the point F and also observing the distractor D. The scale is very small to exaggerate the angles in order to see what they measure at normal viewing distances.
[more]
Contributed by: Keith Stroyan (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This collection of Demonstrations is mainly concerned with describing the geometric inputs to vision that are needed for both static and moving depth perception. There is an outline in the Demonstration "Motion/Pursuit Law in 1D (Visual Depth Perception 1)" (see Related Links).
Permanent Citation