Details

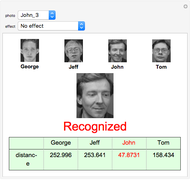
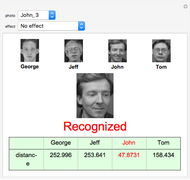
We have a face database of four people with photos of size 112×92 (10304 pixels). We represent each photo as a vector with 10304 elements to form a 10304×4 matrix 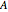. From each element of 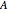we subtract the mean value of the elements from the same row to get a matrix 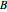. The four eigenvectors of the matrix 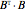are calculated as are the coordinates of every "photo vector" in the basis formed by the eigenvectors.

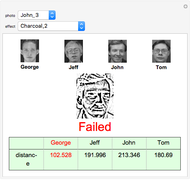
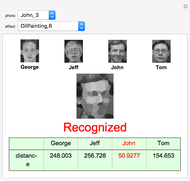
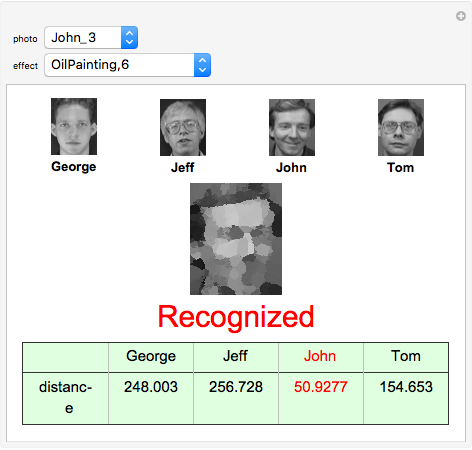
Getting a set of 24 photos (six different photos of every person) we choose one of them, add some image effects if we want, and calculate its coordinates. It will correspond to one of the four photos we have with the minimum "distance" between them. So the given photo will be recognized or not.