Family of Plane Curves in the Extended Gauss Plane Generated by One Function

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
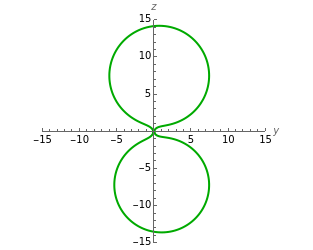
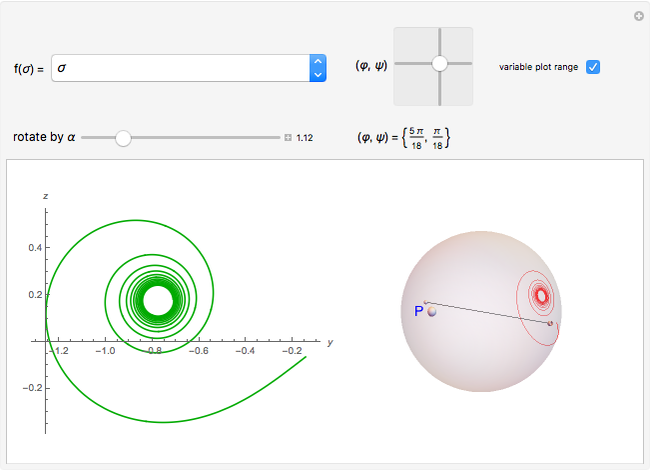
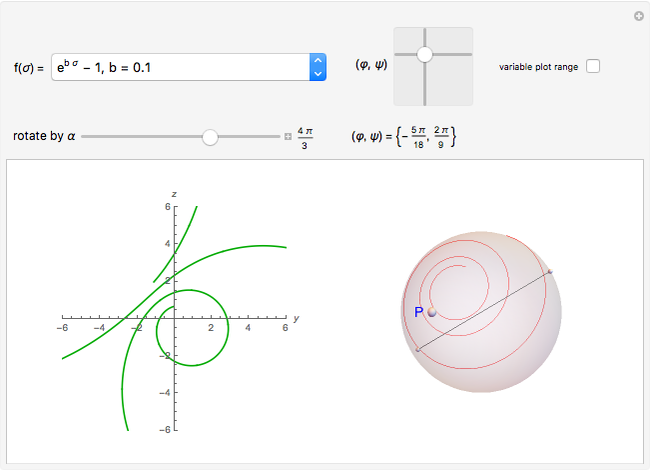
This Demonstration shows four families of curves, each member of which satisfies an equation of the form  , where, at any point on the parametrized curve,
, where, at any point on the parametrized curve,  represents the arc length to that point and
represents the arc length to that point and  represents the spherical curvature at that point when the curve is projected onto the sphere via stereographic projection. If a curve on the sphere can be obtained from another via rotation of the sphere, then the two plane curves that are their stereographic projections are in the same family. The polar coordinates
represents the spherical curvature at that point when the curve is projected onto the sphere via stereographic projection. If a curve on the sphere can be obtained from another via rotation of the sphere, then the two plane curves that are their stereographic projections are in the same family. The polar coordinates  of an arbitrary point on the sphere define an axis of rotation; use that and an angle of rotation
of an arbitrary point on the sphere define an axis of rotation; use that and an angle of rotation  to get different curves in a family.
to get different curves in a family.
Contributed by: Radostina Encheva (July 2013)
Open content licensed under CC BY-NC-SA
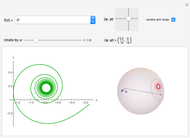
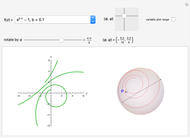
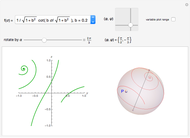
Snapshots
Details
The two-dimensional unit sphere  , centered at the origin, is a model of the Gauss plane together with a point at infinity. This model is realized via a stereographic projection
, centered at the origin, is a model of the Gauss plane together with a point at infinity. This model is realized via a stereographic projection  from the pole
from the pole 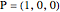 onto the plane
onto the plane 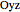 through the equator. The group of rigid motions on
through the equator. The group of rigid motions on  coincides with the group of rotations
coincides with the group of rotations  that preserves
that preserves  . Any spherical curve on
. Any spherical curve on  , parameterized by an arc length parameter
, parameterized by an arc length parameter  , is defined up to a rigid motion on
, is defined up to a rigid motion on  by a function called spherical curvature. The group of rigid motions on
by a function called spherical curvature. The group of rigid motions on  induces on the plane
induces on the plane 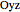 via the stereographic projection a subgroup
via the stereographic projection a subgroup  of the Möbius group. The transformations of this subgroup are represented by the functions
of the Möbius group. The transformations of this subgroup are represented by the functions  ,
, 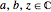 ,
,  , where
, where  is the field of complex numbers. A relation between the spherical curvature
is the field of complex numbers. A relation between the spherical curvature  of a curve on
of a curve on  and the Euclidean curvature of its corresponding plane curve is an invariant under the group
and the Euclidean curvature of its corresponding plane curve is an invariant under the group  and determines any plane curve up to transformation from the group
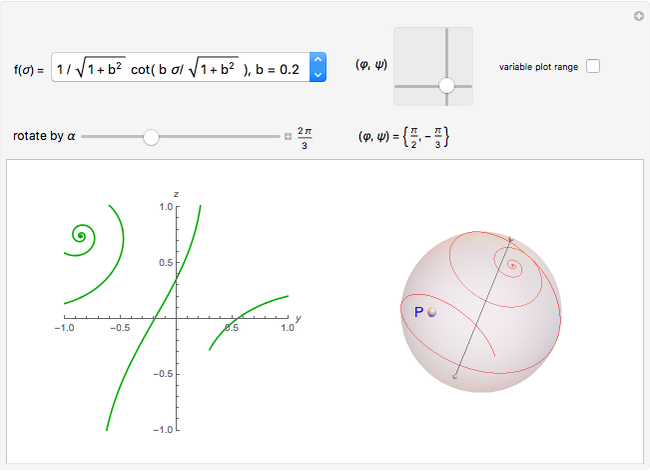
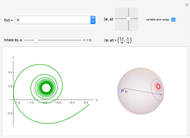
and determines any plane curve up to transformation from the group  . For example, in snapshot 3, the function
. For example, in snapshot 3, the function  defines plane curves equivalent to the logarithmic spiral. Since the natural Cesàro equation for the curvature
defines plane curves equivalent to the logarithmic spiral. Since the natural Cesàro equation for the curvature 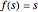 defines a Cornu's spiral in the Euclidean plane, the curve in snapshot 1 could be called a Cornu's spiral in the Möbius plane with a group of rigid motion
defines a Cornu's spiral in the Euclidean plane, the curve in snapshot 1 could be called a Cornu's spiral in the Möbius plane with a group of rigid motion  .
.
Permanent Citation