Farkas's Lemma in Two Dimensions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
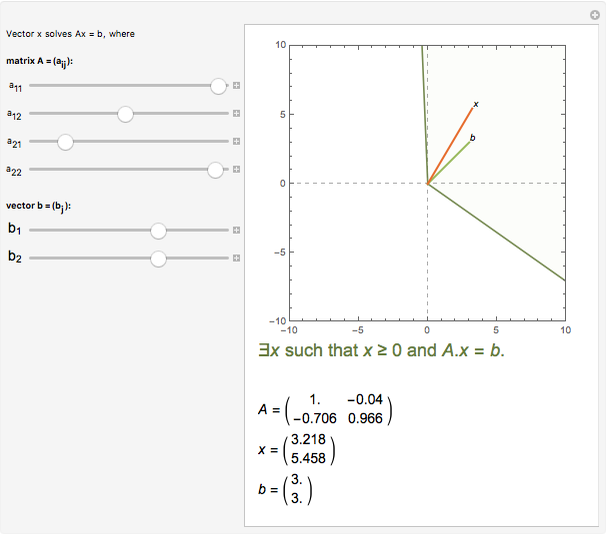
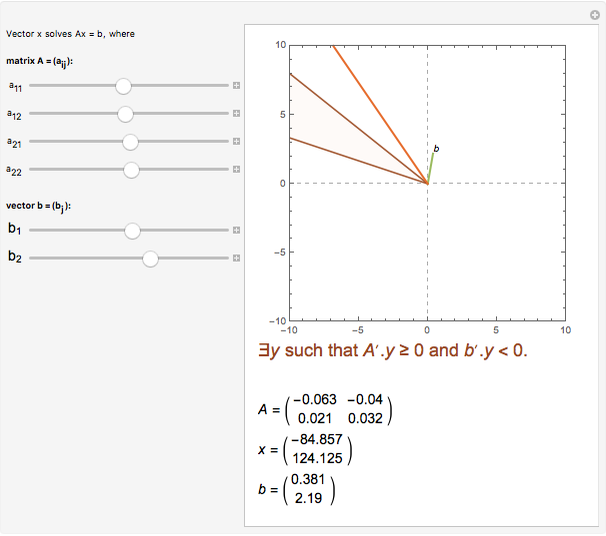
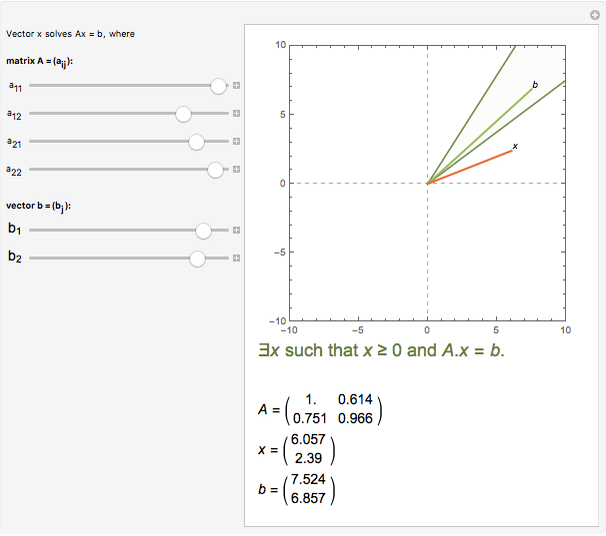
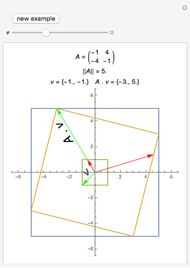
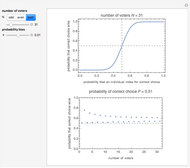
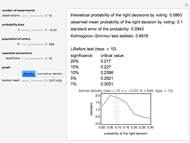
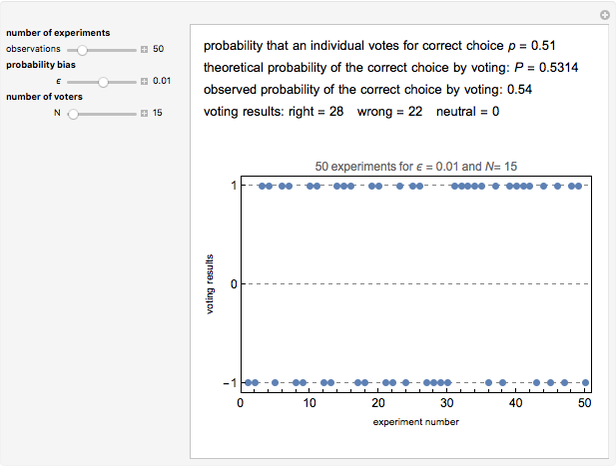
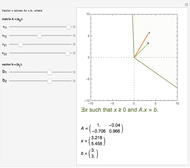
This Demonstration shows a two-dimensional graphical exposition of Farkas's lemma: let 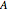 be a
be a 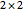 matrix and
matrix and  be a
be a 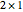 vector. Then either (1) there is a
vector. Then either (1) there is a 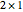 vector
vector  so that
so that 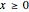 and
and 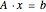 ; or (2) there is a vector
; or (2) there is a vector 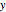 satisfying
satisfying 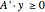 and
and 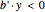 . As is well known, geometrically this statement is equivalent to saying that
. As is well known, geometrically this statement is equivalent to saying that  is either in the cone spanned by
is either in the cone spanned by 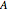 or not. In this Demonstration,
or not. In this Demonstration,  and
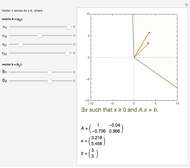
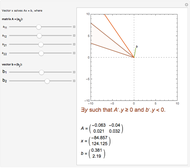
and  are shown by green and orange lines and the inside of the cone is filled with light blue if (1) is true and with light red if (2) is true.
are shown by green and orange lines and the inside of the cone is filled with light blue if (1) is true and with light red if (2) is true.
Contributed by: Tetsuya Saito (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Consider a linear system equation 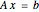 , where
, where 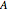 is in general an
is in general an 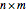 matrix and
matrix and  and
and  are respectively an
are respectively an 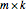 and an
and an 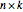 vector. Then Farkas's lemma states that one but not both of the following two statements is true: (1) there is a vector
vector. Then Farkas's lemma states that one but not both of the following two statements is true: (1) there is a vector 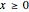 solving the equation; or (2) there is a vector
solving the equation; or (2) there is a vector 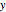 satisfying
satisfying  and
and 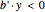 , where
, where  is the zero vector. Geometrically, this is equivalent to saying that: (1)
is the zero vector. Geometrically, this is equivalent to saying that: (1)  is in the cone
is in the cone 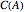 spanned by
spanned by 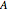 ; or (2)
; or (2)  is not in
is not in 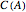 . To show the equivalence is simple. The first statement requires directly that
. To show the equivalence is simple. The first statement requires directly that  is in
is in 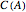 , so that
, so that 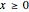 . If (1) does not hold, then
. If (1) does not hold, then  is not in
is not in 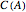 ; therefore, we will find a separating hyperplane between
; therefore, we will find a separating hyperplane between 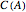 and
and  . In that case, we can find a vector
. In that case, we can find a vector 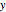 whose angles with each row of
whose angles with each row of 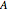 are at most
are at most 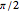 . Because such a
. Because such a 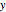 is included in
is included in 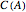 , its angle with
, its angle with  must be greater than
must be greater than 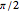 . In order to understand this lemma intuitively, it is more or less sufficient to understand the two-dimensional case.
. In order to understand this lemma intuitively, it is more or less sufficient to understand the two-dimensional case.
Permanent Citation