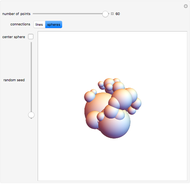
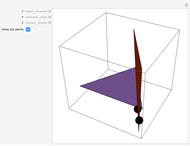
Fate of the Euler Line and the Nine-Point Circle on the Sphere

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
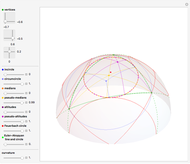
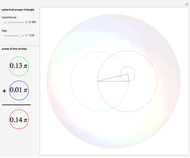
In Euclidean geometry, the circumcenter, the centroid and the orthocenter of a triangle always lie on a line called the Euler line. Correspondingly, the midpoints of the sides, the feet of the altitudes and the midpoints between the vertices and the orthocenter lie on a circle called the nine-point or Euler circle. The nine-point circle is tangent to the incircle and to the excircles of the triangle, and its center also lies on the Euler line. These results do not apply unchanged to spherical geometry.
[more]
Contributed by: Paolo Maraner (March 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
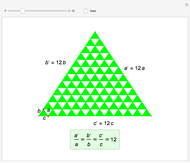
In 1767, Euler [1] discovered that three of the four classical centers—circumcenter, centroid and orthocenter—of every Euclidean triangle always lie on a line, now called the Euler line. Later, Brianchon and Poncelet (1821) and Feuerbach (1822) discovered that the three midpoints of the sides and the three feet of the altitudes lie on a circle, the six-point circle. Feuerbach also proved that this circle is internally tangent to the incircle and externally tangent to the excircles of the triangle. Davies (1827) showed that the center of the six-point circle lies on the Euler line. Eventually, Terquem (1842) recognized that the circle also passes through the midpoints between the triangle's vertices and the orthocenter, thus he renamed it the nine-point circle [2]. The nine-point circle is also known as the Euler circle.
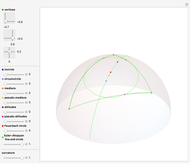
In spherical geometry, the circumcenter, centroid and orthocenter are in general noncollinear. The three circles passing through
1. the three midpoints of the sides,
2. the three feet of the altitudes and
3. the three midpoints between the triangle's vertices and the orthocenter
and the Feuerbach circle (the circle tangent to incircle and excircles) are different in general.
Nonetheless, there are infinitely many triangle centers that reduce to the same center in the Euclidean limit [5]. In particular, the intersection of the three medians and the intersection of the three line segments dividing the triangle into two equal-area triangles coincides in Euclidean geometry, but not in spherical geometry. Analogously, the intersection of the three altitudes and the intersection of the three line segments dividing the triangle into two triangles with adjacent base angles equal to the sum of the other two angles diminished by half of the spherical excess of the whole triangle, a possible generalization of "right triangle" to spherical geometry [3, 4], coincides in Euclidean geometry, but not in spherical geometry.
Akopyan [6] named these line segments pseudo-medians and pseudo-altitudes, respectively, of the spherical triangle. He proved that the relative concurrence points, the pseudo-centroid and pseudo-orthocenter, are collinear with the circumcenter. Moreover, he proved that the feet of pseudo-medians and pseudo-altitudes lie on a circle that is tangent to the incircle and to the excircles of the spherical triangle and whose center also lies on the same line.
This generalizes the Euler line, the nine-point circle and the Feuerbach theorem to spherical geometry.
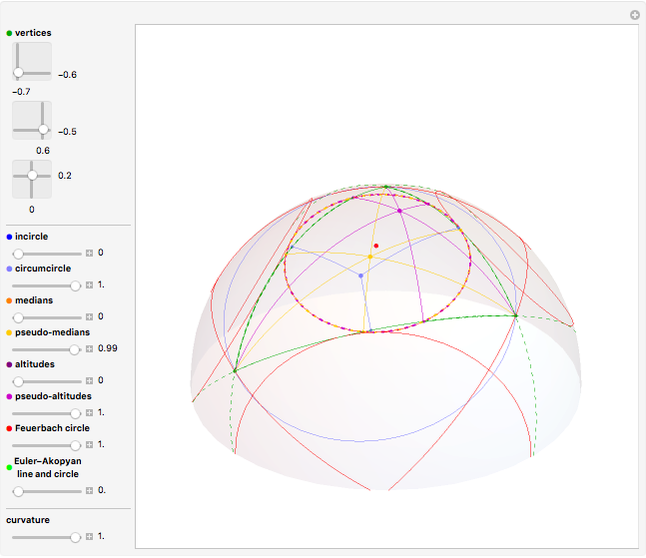
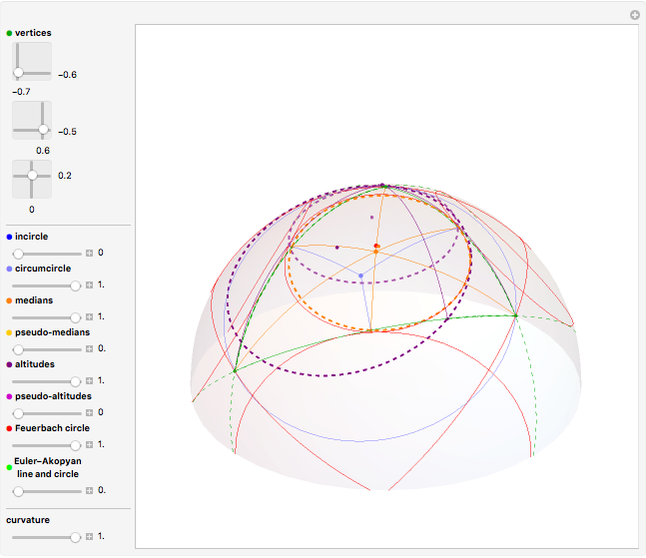
Incircle
The three angle bisectors of a triangle are concurrent in a point, the incenter of the triangle. The incenter is the center of the incircle, the circle tangent to the three sides of the triangle.
Circumcircle
The three perpendicular side bisectors of a triangle are concurrent in a point, the circumcenter of the triangle. The circumcenter is the center of the circumcircle, the circle passing through the three vertices of the triangle.
Medians
The medians are the lines connecting the vertices of a triangle to the midpoints of the opposite sides. In Euclidean geometry, each median divides the triangle into two equal-area triangles. The three medians are concurrent in a point, the centroid of the triangle. The medial circle is the circle passing through the three midpoints of the sides. In Euclidean geometry, it coincides with the nine-point circle.
Pseudo-medians
The pseudo-medians, or area-bisecting cevians, are the line segments dividing the triangle into two equal-area triangles. The three pseudo-medians are concurrent in a point, the pseudo-centroid of the triangle. In Euclidean geometry, the pseudo-medians and the pseudo-centroid coincide with the medians and the centroid, respectively. The pseudo-medial circle is the circle passing through the three feet of the pseudo-medians. It always coincides with the pseudo-orthic circle and with the Feuerbach circle of the triangle.
Altitudes
The altitudes are the lines through the vertices of a triangle and orthogonal to the opposite sides. Equivalently, they are the lines dividing the triangle into two triangles with adjacent base angles equal to the sum of the other two angles, 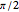 . The three altitudes are concurrent in a point, the orthocenter of the triangle. The orthic circle is the circle passing through the three feet of the altitudes. In Euclidean geometry, it coincides with the nine-point circle. In Euclidean geometry, the circle passing through the midpoints between the triangle's vertices and the orthocenter also coincides with the nine-point circle.
. The three altitudes are concurrent in a point, the orthocenter of the triangle. The orthic circle is the circle passing through the three feet of the altitudes. In Euclidean geometry, it coincides with the nine-point circle. In Euclidean geometry, the circle passing through the midpoints between the triangle's vertices and the orthocenter also coincides with the nine-point circle.
Pseudo-altitudes
The pseudo-altitudes are the line segments dividing the triangle into two triangles with adjacent base angles equal to the sum of the other two angles diminished by half of the spherical excess of the whole triangle. The three pseudo-altitudes are concurrent in a point, the pseudo-orthocenter of the triangle. In Euclidean geometry, the pseudo-altitudes and the pseudo-orthocenter coincide with the altitudes and the orthocenter, respectively. The pseudo-orthic circle is the circle passing through the three feet of the pseudo-altitudes. It always coincides with the pseudo-medial circle and with the Feuerbach circle of the triangle.
Excircles and Feuerbach Circle
The internal and external angle bisectors of a triangle are concurrent in three points, the excenters of the triangle. They are the centers of the excircles, the circles tangent to one side and to the other two sides of the triangle extended. The Feuerbach circle is the circle externally tangent to the three excircles. It is also internally tangent to the incircle of the triangle. In Euclidean geometry, the Feuerbach circle corresponds to the nine-point circle of the triangle. It always coincides with the pseudo-medial and pseudo-orthic circles of the triangle.
References
[1] L. Euler, "Solutio facilis problematum quorundam geometricorum difficillimorum," Novi Commentarii Academiae Scientiarum Petropolitanae, 11, 1765 (1767) pp. 103–123.
[2] J. S. MacKay, "History of the Nine Point Circle," Proceedings of the Edinburgh Mathematical Society, 11, 1892 pp. 19–61.
[3] W. Dickinson and M. Salmassi, "The 'Right' Right Triangle on the Sphere," College Mathematics Journal, 39(1), 2008 pp. 24–33.
[4] P. Maraner, "A Spherical Pythagorean Theorem," The Mathematical Intelligencer, 32(3), 2010 pp. 46–50. doi:10.1007/s00283-010-9152-9.
[5] R. A. Russell, "Non-Euclidean Triangle Centers." arxiv.org/abs/1608.08190.
[6] A. V. Akopyan, "On Some Classical Constructions Extended to Hyperbolic Geometry." arxiv.org/abs/1105.2153.
Permanent Citation
"Fate of the Euler Line and the Nine-Point Circle on the Sphere"
http://demonstrations.wolfram.com/FateOfTheEulerLineAndTheNinePointCircleOnTheSphere/
Wolfram Demonstrations Project
Published: March 3 2017