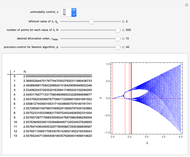
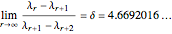Feigenbaum's Scaling Relation for Superstable Parameter Values: "Bifurcation Diagram Helper"

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
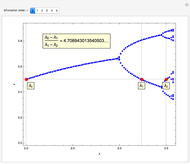
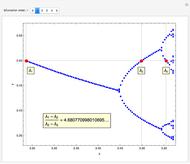
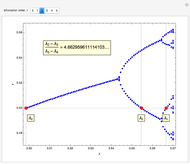
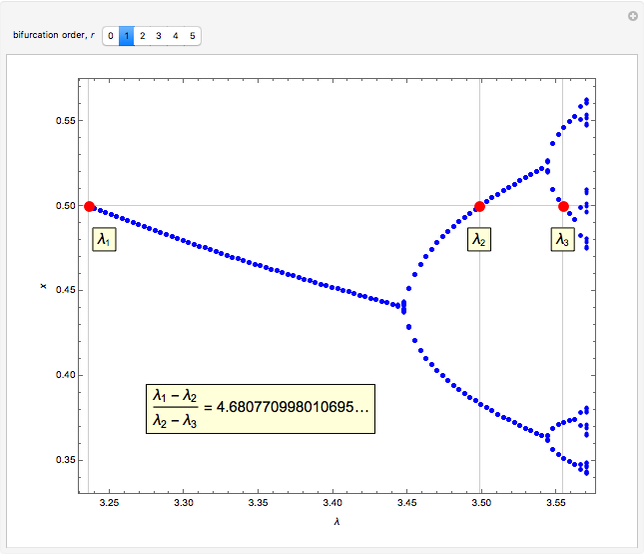
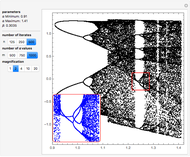
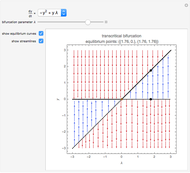
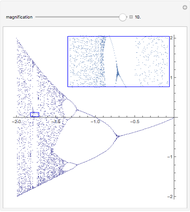
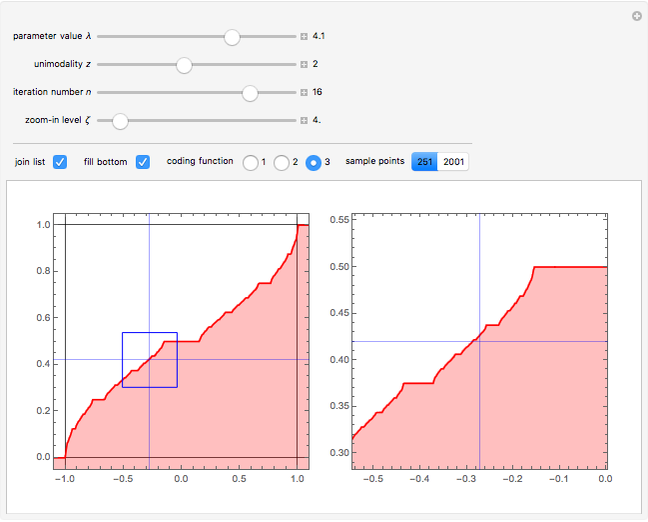
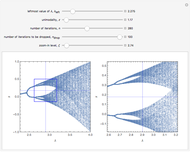
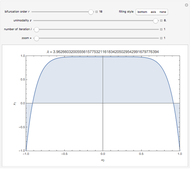
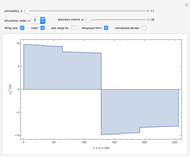
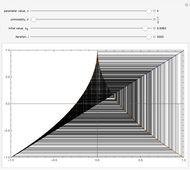
As the fixed points of the iterated function 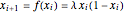 approach chaotic behavior with repeated period doubling, the superstable parameter value
approach chaotic behavior with repeated period doubling, the superstable parameter value 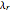 approaches its limiting value
approaches its limiting value 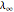 , known as the Feigenbaum point. As the value of
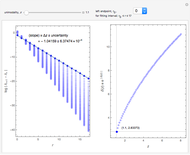
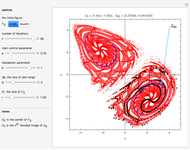
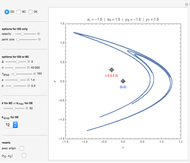
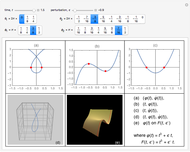
, known as the Feigenbaum point. As the value of  (the order of the period-doubling bifurcation) increases, Feigenbaum's scaling relation between the three adjacent superstable parameter values approaches a universal limit
(the order of the period-doubling bifurcation) increases, Feigenbaum's scaling relation between the three adjacent superstable parameter values approaches a universal limit 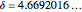 known as Feigenbaum's constant [1–7], that is,
known as Feigenbaum's constant [1–7], that is,
Contributed by: Ki-Jung Moon (October 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] K. T. Alligood, T. D. Sauer, and J. A. Yorke, Chaos: An Introduction to Dynamical Systems, New York: Springer, 1996.
[2] S. H. Strogatz, Nonlinear Dynamics and Chaos, New York: Perseus Books Publishing, 1994.
[3] S. Wolfram, A New Kind of Science, Champaign, IL: Wolfram Media, 2002.
[4] M. J. Feigenbaum, "Quantitative Universality for a Class of Non-Linear Transformations," Journal of Statistical Physics, 19, 1978 pp. 25–52.
[5] M. J. Feigenbaum, "The Universal Metric Properties of Nonlinear Transformations," Journal of Statistical Physics, 21, 1979 pp. 669–706.
[6] K.-J. Moon, "Reducible Expansions and Related Sharp Crossovers in Feigenbaum's Renormalization Field," Chaos: An Interdisciplinary Journal of Nonlinear Science, 18, 2008 pp. 023104.
[7] K.-J. Moon, "Erratum: Reducible Expansions and Related Sharp Crossovers in Feigenbaum's Renormalization Field," Chaos: An Interdisciplinary Journal of Nonlinear Science, 20, 2010 pp. 049902.
Permanent Citation