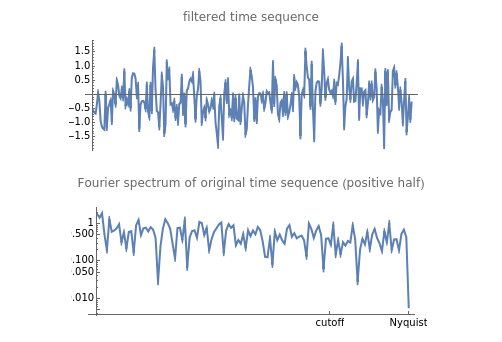
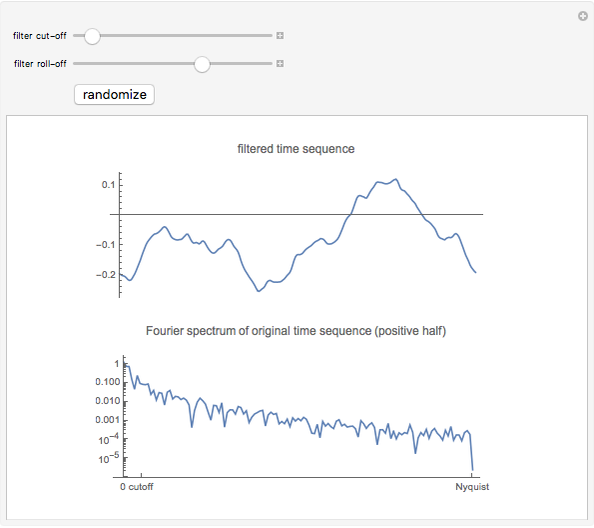
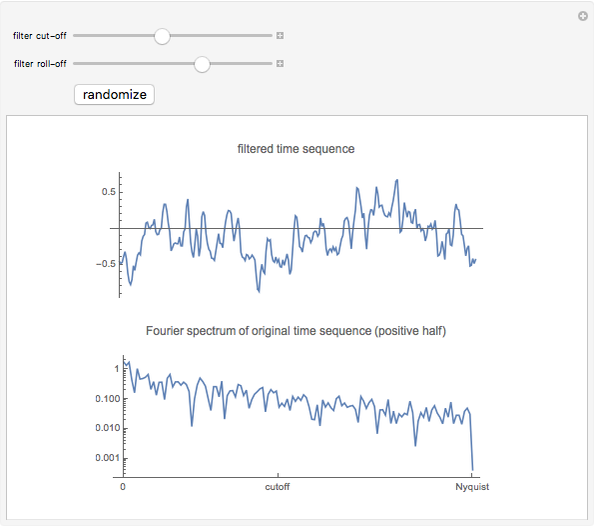
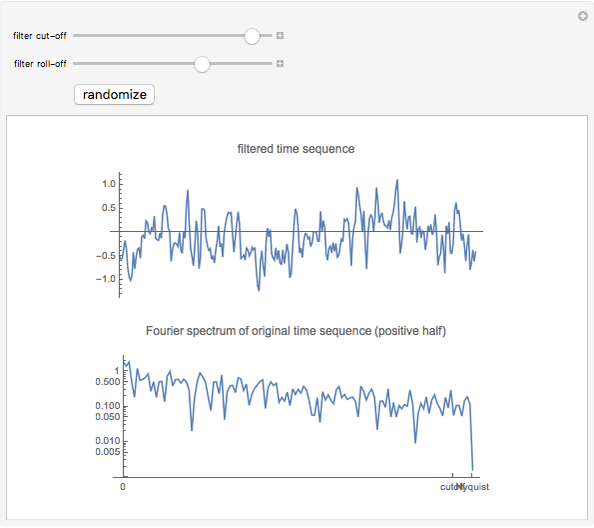
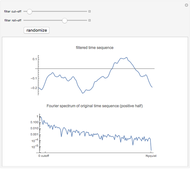
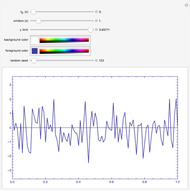
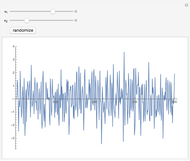
This Demonstration creates a white-noise sequence and then uses a low-pass filter to produce a red-noise sequence. The "filter cut-off" is the fractional point in [0, 1] on the spectral frequency axis to apply the filter, as measured from zero frequency. The rate of suppression of frequencies larger than the filter cut-off is given by the "filter roll-off" exponent (1 to 4); larger values of mean greater suppression of the higher frequencies. A new time sequence is generated with the "randomize" button. The amplitude spectrum of the time series is plotted simultaneously, with spectral values on a log scale, out to the Nyquist frequency.