Finding the Shortest Traveling Salesman Tour

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
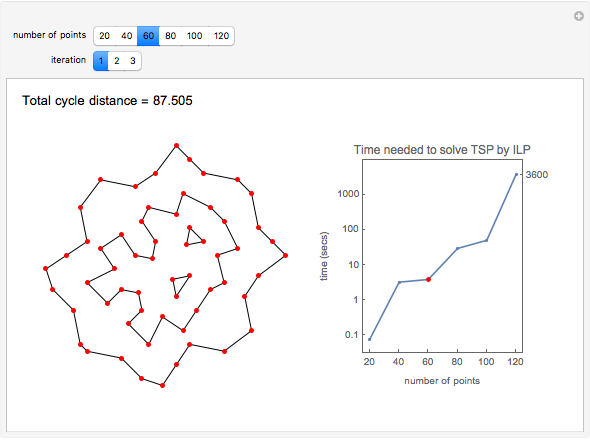
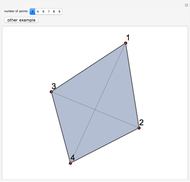
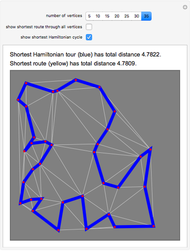
For sets of points that are not too large one can solve the traveling salesman problem—find the shortest cycle that visits all the points—by using integer linear programming (ILP), available in Mathematica via the Minimize function. Given  points, introduce a variable
points, introduce a variable 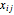 for each possible edge,
for each possible edge,  , the idea being that
, the idea being that 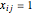 means that one goes from
means that one goes from 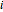 to
to 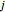 in the tour. Then create the equations that force
in the tour. Then create the equations that force 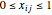 and that each vertex has degree exactly 2, and use the objective function that sums the product of the distances between points with
and that each vertex has degree exactly 2, and use the objective function that sums the product of the distances between points with 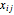 .
.
Contributed by: Stan Wagon (Macalester College) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
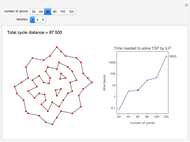
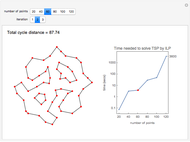
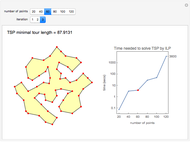
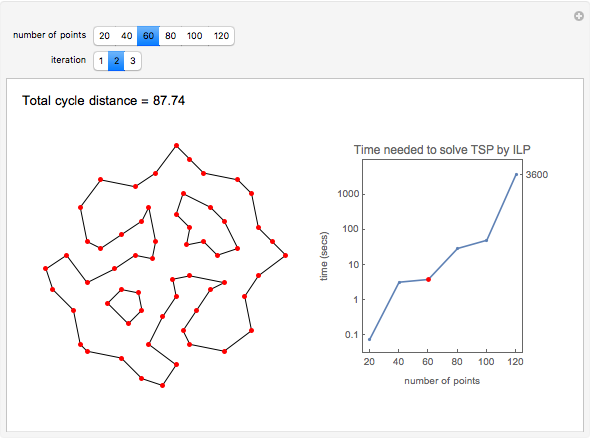
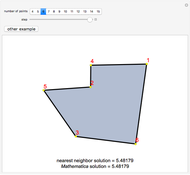
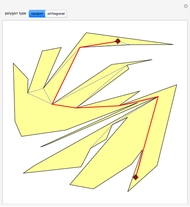
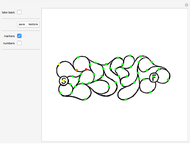
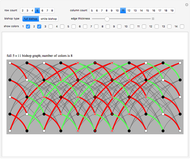
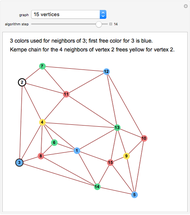
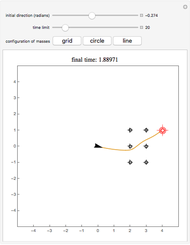
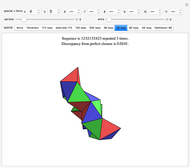
The snapshots show the three iterations required to find the optimal solution in the case of 60 points; that requires only three seconds.
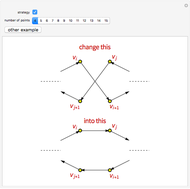
The equations used to set the degrees are: 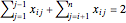 for each
for each 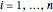 . The inequality used to break a cycle
. The inequality used to break a cycle 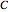 is:
is: 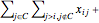
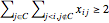 . The objective function that is minimized is:
. The objective function that is minimized is: 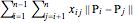 , where
, where 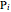 is the
is the 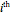 point.
point.
For more details, see Chapter 13 of S. Wagon, Mathematica in Action, 3rd ed., New York, Springer, 2010.
Permanent Citation