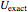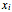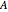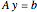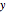Finite Element Solution of 1D Poisson Equation with Galerkin Spectral Decomposition

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
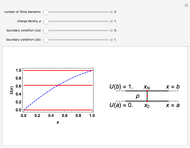
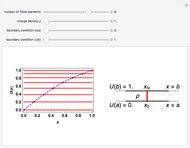
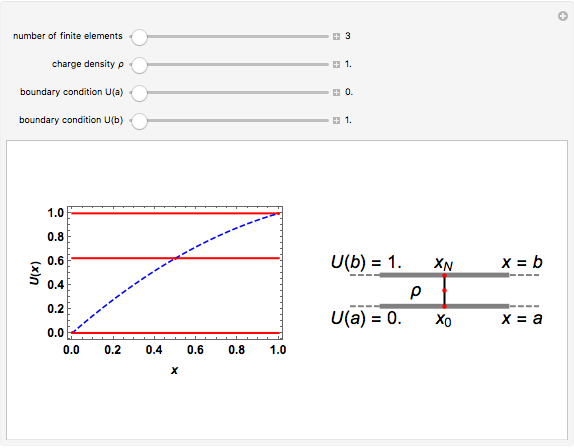
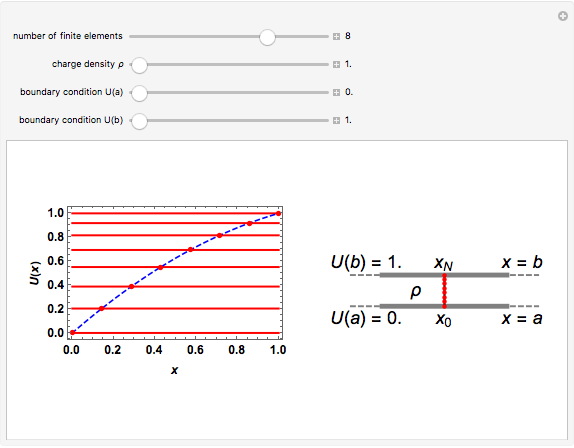
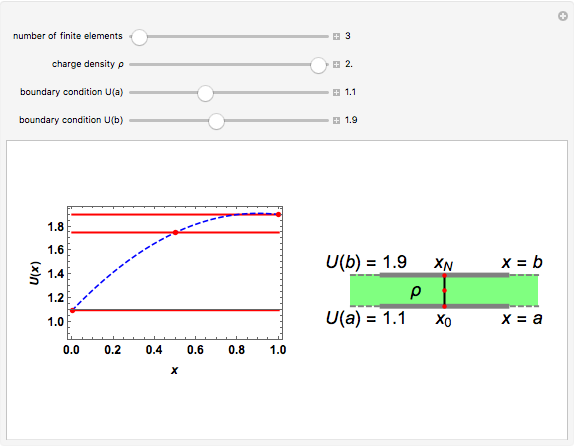
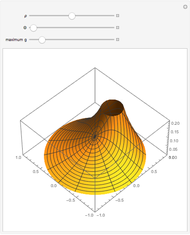
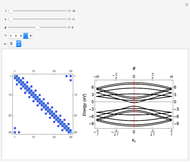
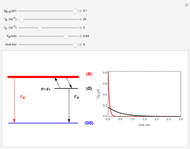
This Demonstration shows the finite element method (FEM) applied to the solution of the 1D Poisson equation. A capacitor with plates at a fixed distance 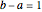 with each plate held at potential
with each plate held at potential  and
and  , respectively, is shown on the right. The 1D Poisson equation for the potential
, respectively, is shown on the right. The 1D Poisson equation for the potential is
is 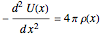 , with the charge density
, with the charge density  between the plates in the range
between the plates in the range 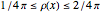 for simplicity. The solution
for simplicity. The solution 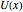 over the entire domain
over the entire domain 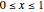 is subject to the Dirichlet boundary conditions (BCs):
is subject to the Dirichlet boundary conditions (BCs): 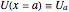 and
and 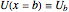 .
.
Contributed by: Jessica Alfonsi (University of Padova, Italy) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The Mathematica program here has been adapted and extended from the Java code LaplaceFEM.java in the following book:
R. H. Landau, M. J. Paez, and C. C. Bordeianu, A Survey of Computational Physics, Princeton: Princeton University Press, 2008.
A standard reference for the basics of the finite-element method applied to electromagnetics is, for instance:
J. Jin, The Finite Element Method in Electromagnetics, 2nd. ed., New York: John Wiley and Sons, 2002.
Permanent Citation