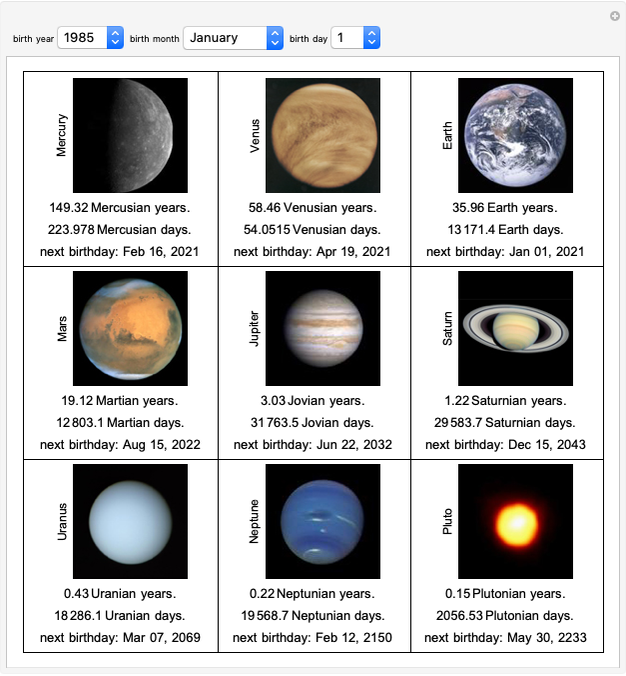
Finite-State, Discrete-Time Markov Chains

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
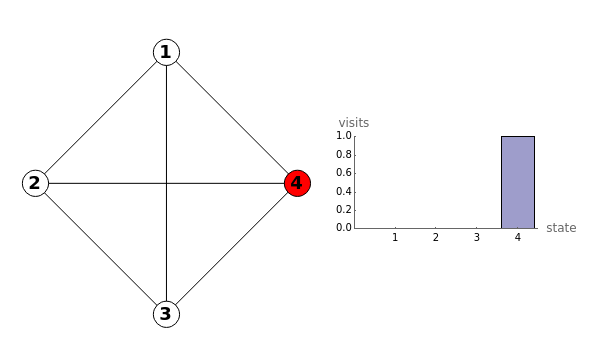
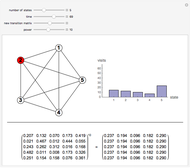
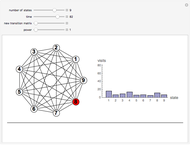
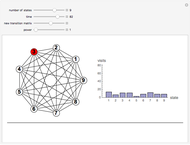
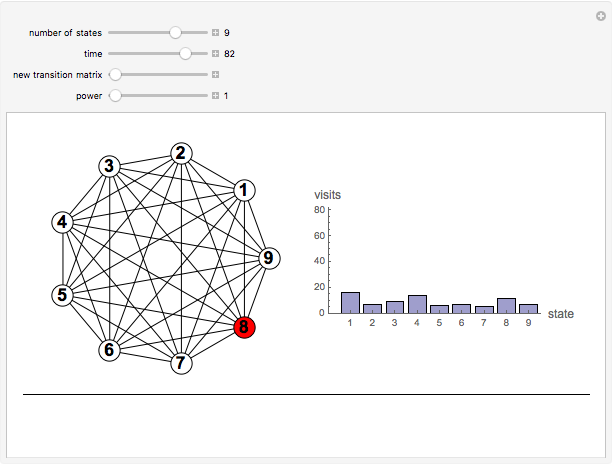
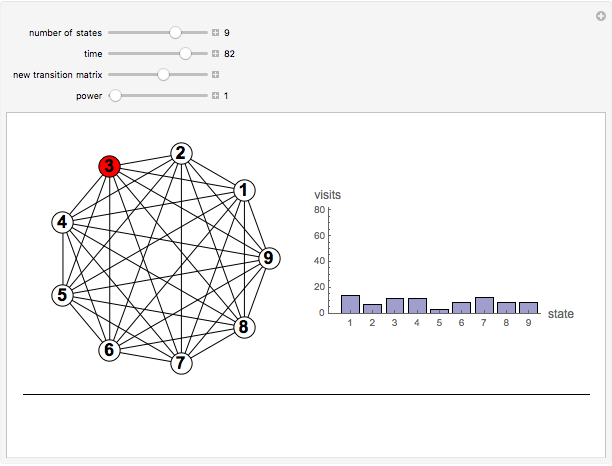
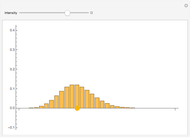
Consider a system that is always in one of  states, numbered 1 through
states, numbered 1 through  . Every time a clock ticks, the system updates itself according to an
. Every time a clock ticks, the system updates itself according to an  matrix of transition probabilities, the
matrix of transition probabilities, the  entry of which gives the probability that the system moves from state
entry of which gives the probability that the system moves from state  to state
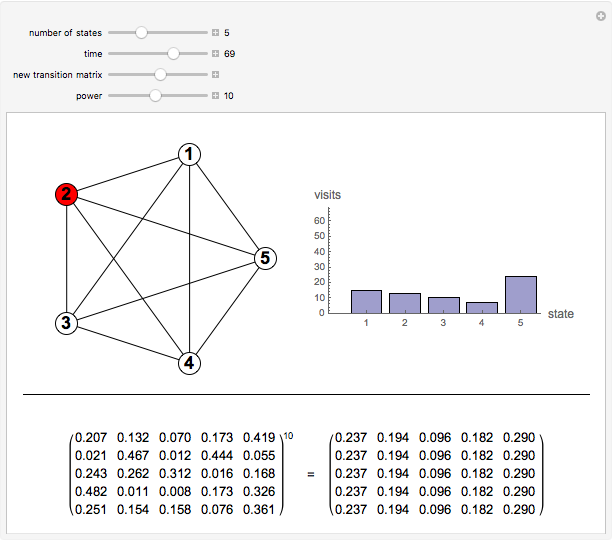
to state 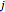 at any clock tick. A Markov chain is a system like this, in which the next state depends only on the current state and not on previous states. Powers of the transition matrix approach a matrix with constant columns as the power increases. The number to which the entries in the
at any clock tick. A Markov chain is a system like this, in which the next state depends only on the current state and not on previous states. Powers of the transition matrix approach a matrix with constant columns as the power increases. The number to which the entries in the  column converge is the asymptotic fraction of time the system spends in state
column converge is the asymptotic fraction of time the system spends in state  .
.
Contributed by: Chris Boucher (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Finite-State, Discrete-Time Markov Chains"
http://demonstrations.wolfram.com/FiniteStateDiscreteTimeMarkovChains/
Wolfram Demonstrations Project
Published: March 7 2011