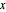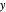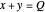Firm with Two Plants

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
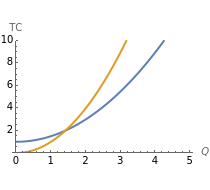
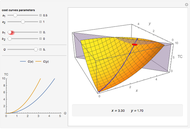
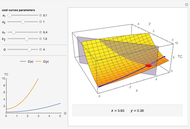
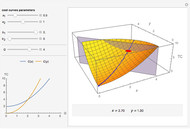
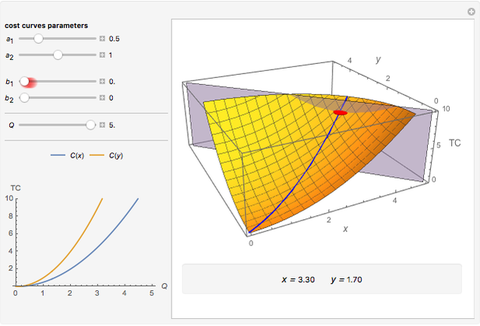
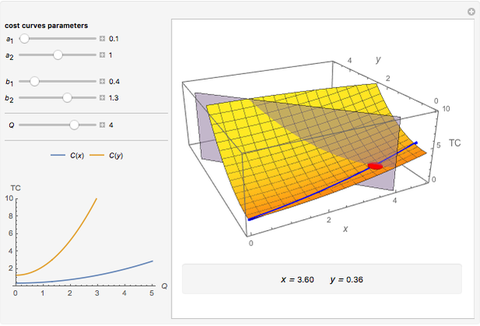
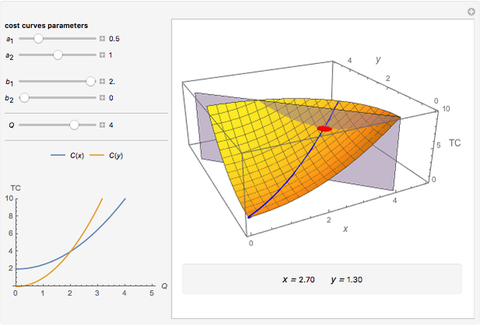
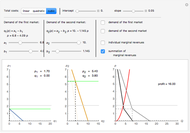
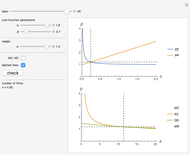
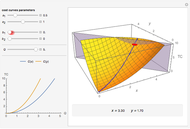
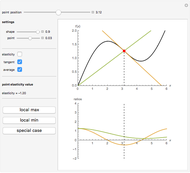
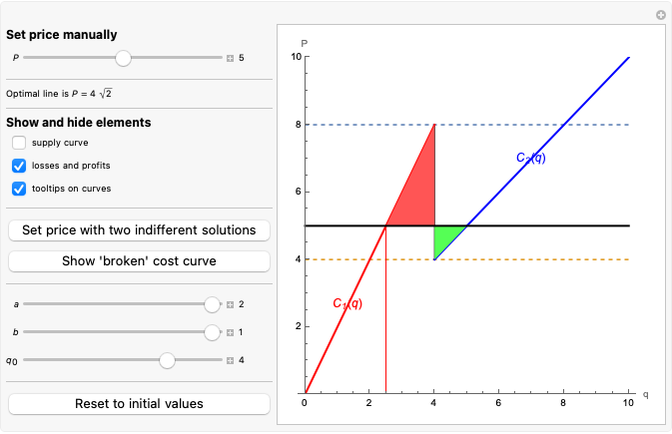
This Demonstration shows how to distribute the production of uniform goods between two or more (generally many) plants that have different total cost (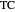 ) functions. Put differently, it shows how to minimize total production costs of several plants subject to a given total production plan
) functions. Put differently, it shows how to minimize total production costs of several plants subject to a given total production plan 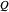 .
.
Contributed by: Timur Gareev (April 2018)
Open content licensed under CC BY-NC-SA
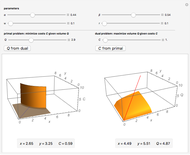
Snapshots
Details
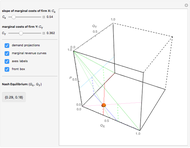
The blue line in the 3D plot shows all optimal production combinations for different values of  . Fixed costs in either plant (denoted as
. Fixed costs in either plant (denoted as 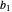 and
and 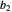 , respectively) do not affect the distribution of production, which is logical because the sum of fixed costs exists even if no output is produced. At the same time, if the variable part of the costs for a plant are relatively lower, that plant starts to produce relatively more of the total output, all other things being equal.
, respectively) do not affect the distribution of production, which is logical because the sum of fixed costs exists even if no output is produced. At the same time, if the variable part of the costs for a plant are relatively lower, that plant starts to produce relatively more of the total output, all other things being equal.
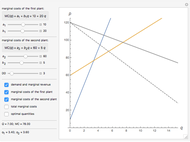
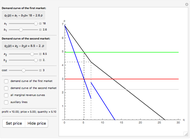
This Demonstration deals with total cost, while the Demonstration "Monopoly with Two Plants" deals with marginal costs. As we may always get marginal costs from total costs, this Demonstration deals with a more general case that is solved as follows:
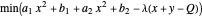 .
.
By differentiating with respect to 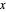 and
and 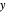 , this expression gives a system of two equations in two unknowns:
, this expression gives a system of two equations in two unknowns:
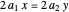 ,
,
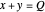 .
.
Here 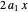 is, in fact, the marginal cost of the first plant and
is, in fact, the marginal cost of the first plant and 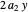 that of the second plant. The equation is the equality of marginal costs for each plant.
that of the second plant. The equation is the equality of marginal costs for each plant.
So, we have a solution:
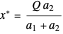 ,
,
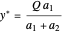 .
.
Permanent Citation