Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Fisher-Tippett-Gnedenko Theorem: Generalizing Three Types of Extreme Value Distributions

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

The extreme value theorem (EVT) in statistics is an analog of the central limit theorem (CLT). The idea of the CLT is that the average of many independently and identically distributed (iid) random variables converges to a normal distribution provided that each random variable has finite mean and variance. Instead of dealing with the central tendency (the mean of the parent distribution), EVT deals with the tailed region of the parent distribution.

[more]

Put simply, EVT expresses the idea that the maximum of iid random variables drawn from a parent distribution converges (in the limit of a very large sample) to one of the three possible tailed distributions, depending on the tailed index of the parent distribution: type I Gumbel distribution (), type II Frechet distribution (), or type III reversed Weibull distribution ().

The boundary of the tailed distribution depends on the tail index of the parent distribution. Thus, a light-tailed () parent distribution places no bound on the maxima (tailed) distribution (type I Gumbel). A heavy-tailed () parent puts a lower bound on the tail, whereas the lightest-tailed () parent imposes an upper bound on the tail (type III reversed Weibull).

[less]

Contributed by: Pichet Thiansathaporn (June 2012)
Open content licensed under CC BY-NC-SA

Snapshots

Details

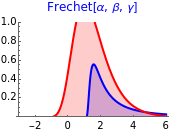
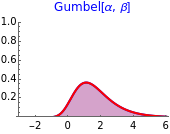
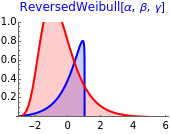
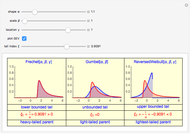
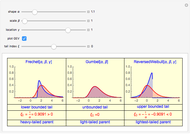
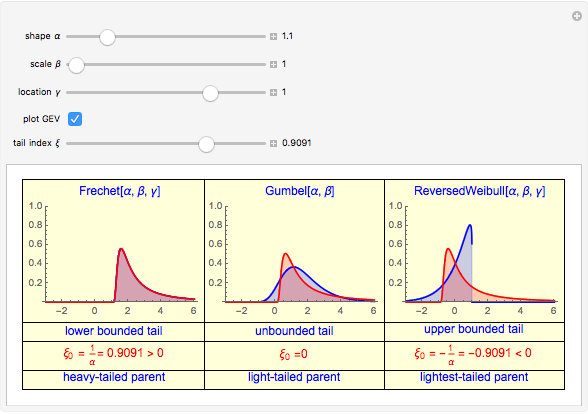
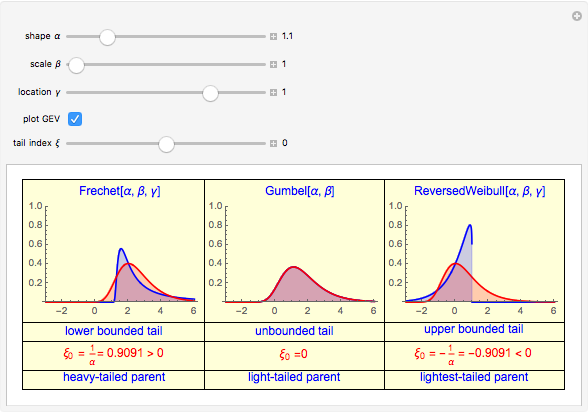
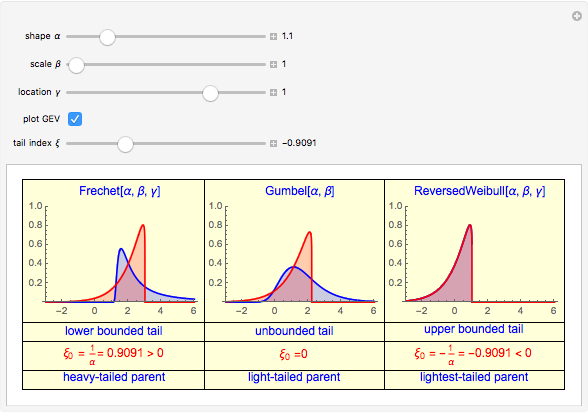
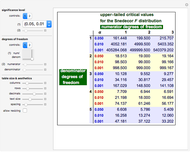
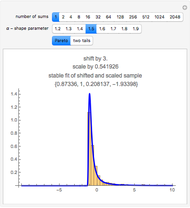
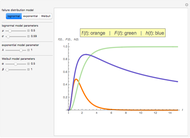
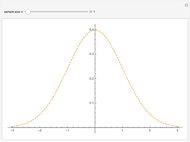
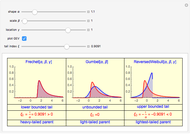
All three families of tailed distributions are subsumed under the generalized extreme value (GEV) distribution, which this Demonstration seeks to illustrate. With the appropriate choice of the tailed index , the probability density function (PDF) of the GEV distribution is equivalent to the PDF of one of the three tailed distributions. The PDF of the GEV distribution (red curve) coincides with one of the three tailed distributions as the slider control sweeps through the appropriate value of the tail index .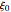

snapshot 1: 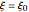(Frechet) causing GEV (red curve) to overlap with the Frechet PDF (blue curve, column 1)

snapshot 2: (Gumbel) causing GEV (red curve) to overlap with the Gumbel PDF (blue curve, column 2)

snapshot 3: (reversed Weibull) causing GEV (red curve) to overlap with the reversed Weibull PDF (blue curve, column 3)

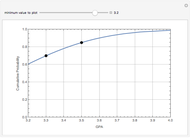
EVT is useful in financial risk management practice because one of the chief concerns is estimating the maximum possible losses in the value of a portfolio, where the lack of historical data makes prediction of future losses unreliable. Of the three types of loss distribution, type II Frechet distribution is especially useful since empirical data shows that portfolio losses exhibit a heavier tail than the normal distribution, thus providing a useful estimate on the lower bound of the tail, whereas type III Weibull distribution is of limited use due to its lightest-tailed nature and for imposing an (unrealistic) upper bound on the tail loss.

The three types of extreme value distributions are special cases of GEV distribution. Their PDFs are related through the following substitutions of variables and parameters:

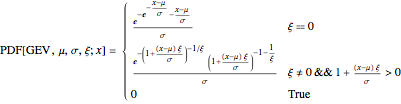
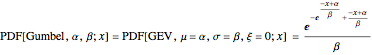
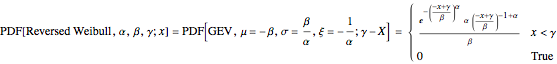
Reference

[1] K. Dowd, Measuring Market Risk, 2nd ed., West Sussex, England: Wiley, 2005 pp. 190–194.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send