Fit of First-Order Kinetic Model in Degradation Processes

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
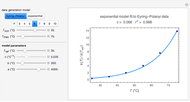
Many chemical, biochemical, and biological degradation processes follow first-order kinetics, which is characterized by a single exponential rate constant. In this Demonstration, we evaluate the possibility that the same experimental data can also be fitted with a general fixed-order kinetic model or with the stretched exponential (Weibull) model with  , which implies either a different order or nonlinear kinetics. This is done by generating data using the first-order kinetics model, with and without added random scatter of a chosen amplitude. The data is then fitted to these alternative models, varying the value of
, which implies either a different order or nonlinear kinetics. This is done by generating data using the first-order kinetics model, with and without added random scatter of a chosen amplitude. The data is then fitted to these alternative models, varying the value of  . It is shown that there might be numerous situations in which first-order kinetics and the two alternative models with
. It is shown that there might be numerous situations in which first-order kinetics and the two alternative models with 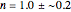 give indistinguishable results.
give indistinguishable results.
Contributed by: Mark D. Normandand Micha Peleg (January 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Snapshot 1: the fit of the stretched exponential (Weibull) model with 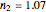 to slightly scattered simulated data
to slightly scattered simulated data
Snapshot 2: the fit of the fixed-order kinetic model with  to highly scattered data generated with a low
to highly scattered data generated with a low 
Snapshot 3: the fit of the stretched exponential (Weibull) model with 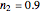 to highly scattered data generated with a low
to highly scattered data generated with a low 
A degradation reaction kinetics order  is defined by the differential equation
is defined by the differential equation  , where
, where 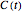 is the concentration at time
is the concentration at time  and
and  is the rate constant with dimensions and units commensurate with
is the rate constant with dimensions and units commensurate with  . The boundary condition is
. The boundary condition is  , the initial concentration.
, the initial concentration.
For first-order kinetics with  , the equation's solution is
, the equation's solution is 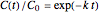 , where the exponential rate constant
, where the exponential rate constant  has units of reciprocal time.
has units of reciprocal time.
For 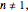 the rate equation's solution is
the rate equation's solution is 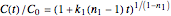 . Theoretically, this solution allows for negative concentration values for certain times when
. Theoretically, this solution allows for negative concentration values for certain times when  and complex numbers for certain times when
and complex numbers for certain times when 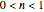 . Replacing these unrealistic values by zero gives a generalized fixed-order kinetics model for
. Replacing these unrealistic values by zero gives a generalized fixed-order kinetics model for 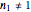 [1], which for
[1], which for 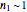 assumes the form
assumes the form 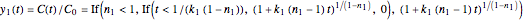 .
.
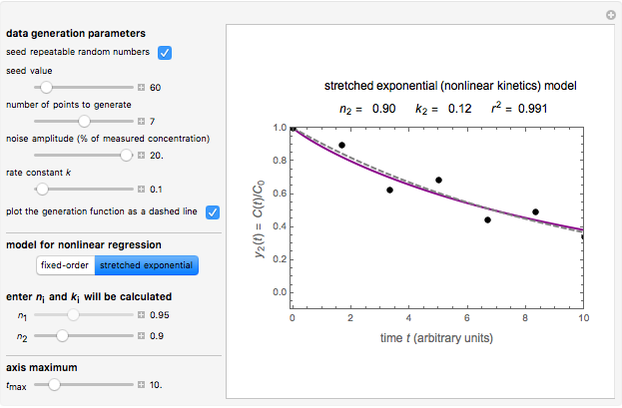
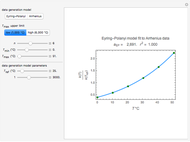
A common model for nonlinear kinetics is the stretched exponential (Weibull) model, of which the first-order is a special case. For our purpose it can be written in the form 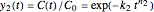 . This model with
. This model with  was shown to be useful in predicting nutrient loss under non-isothermal conditions where, traditionally, first-order kinetics has been used [2, 3].
was shown to be useful in predicting nutrient loss under non-isothermal conditions where, traditionally, first-order kinetics has been used [2, 3].
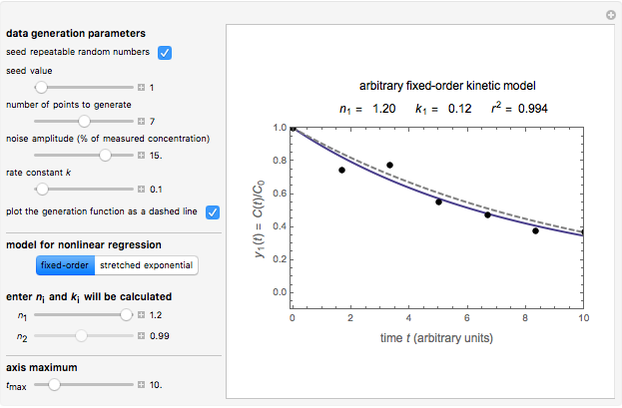
In this Demonstration, you can examine the fit of the three models by generating degradation data with the first-order kinetics model 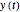 , with or without added random noise, and fitting them by the two other models
, with or without added random noise, and fitting them by the two other models  and
and  using nonlinear regression.
using nonlinear regression.
The model is chosen with a setter bar. The seed, number of data points,  value for their generation, the scatter's amplitude, and the
value for their generation, the scatter's amplitude, and the 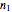 or
or  in
in  and
and  are entered with sliders, as is the maximum of the time axis. By clicking the checkbox, you can select a repeatable seed and choose or decline to plot the generated curve as a dashed curve before the added noise.
are entered with sliders, as is the maximum of the time axis. By clicking the checkbox, you can select a repeatable seed and choose or decline to plot the generated curve as a dashed curve before the added noise.
The Demonstration plots the generated data points on which the fitted curve is superimposed as a solid curve. It also displays the chosen 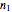 or
or  , calculated
, calculated 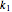 or
or 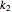 , and the fit's
, and the fit's  -squared value. It shows that with the values of
-squared value. It shows that with the values of 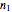 and
and  within the range of 0.8 to 1.2, there can be multiple combinations of the parameters in which the models have a similar fit, as judged by statistical criteria. This suggests that data fit alone might not be sufficient to establish first-order kinetics.
within the range of 0.8 to 1.2, there can be multiple combinations of the parameters in which the models have a similar fit, as judged by statistical criteria. This suggests that data fit alone might not be sufficient to establish first-order kinetics.
References
[1] M. Peleg, M. D. Normand, and A. D. Kim, "Estimating Thermal Degradation Kinetics Parameters from the Endpoints of Non-isothermal Heat Processes or Storage," Food Research International, 66, 2014 pp. 313–324. doi:10.1016/j.foodres.2014.10.003.
[2] M. G. Corradini and M. Peleg, "A Model of Non-isothermal Degradation of Nutrients, Pigments and Enzymes," Journal of the Science of Food and Agriculture, 84(3), 2004 pp. 217–226. doi:10.1002/jsfa.1647.
[3] M. G. Corradini and M. Peleg, "Prediction of Vitamins Loss during Non-isothermal Heat Processes and Storage with Non-linear Kinetic Models," Trends in Food Science & Technology, 17(1), 2006 pp. 24–34. doi:10.1016/j.tifs.2005.09.004.
Permanent Citation