Wolfram Demonstrations Project

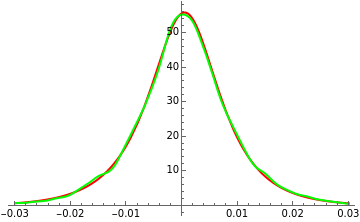
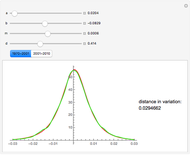
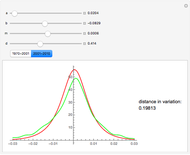
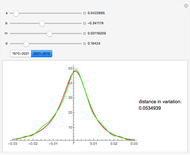
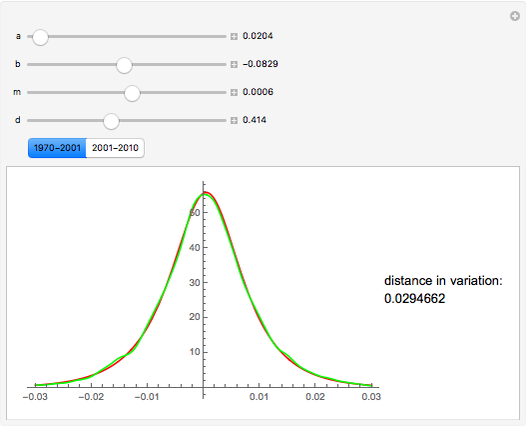
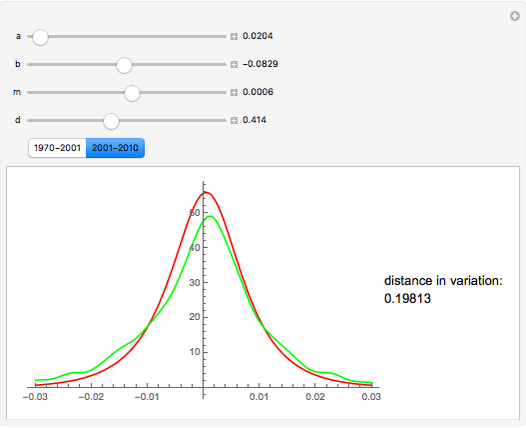
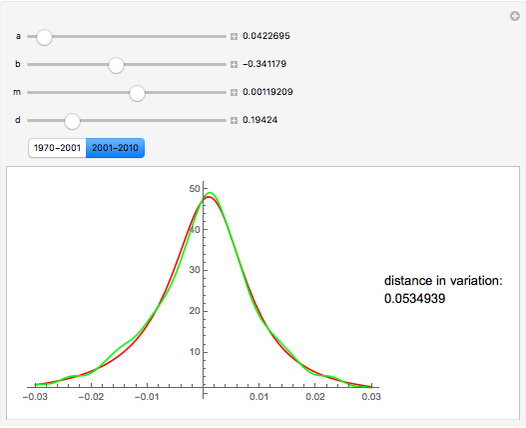
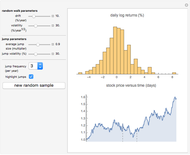
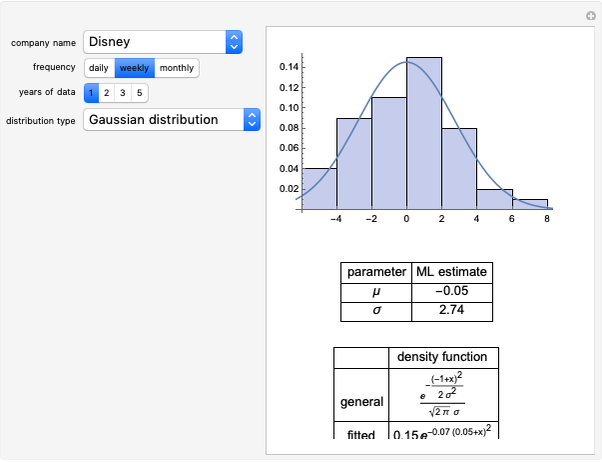
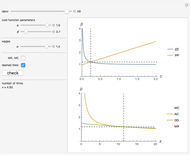
The Meixner process is a Lévy pure jump stochastic process that was introduced into mathematical finance in 2001 by Schoutens. Schoutens showed that the normal distribution provides a very poor fit to the log returns of the S&P 500 index for the years 1970–2001 but that the Meixner distribution (for suitably chosen parameters) provides an excellent fit. In this Demonstration we confirm this and show that, although the parameters found by Schoutens no longer provide as good a fit to the prices for the period 2001–2010, one can use Mathematica to obtain new parameters that provide almost as good a fit to the latter data as Schoutens' values to the earlier ones.

The initial setting shows (in red) the Meixner process fitted to the S&P 500 index (green) using Schoutens' parameters. The fit is almost perfect. To the left of the graph the distance in variation between the two distributions is shown. Choosing the period 2001–2010 from the setter bar shows that Schouten's fit is no longer as good for this decade. However, choosing the "best 2001–2010" bookmark displays a nearly-as-good fit for the later period, using new values of the parameters.

Contributed by: Andrzej Kozlowski

Slider Zoom
Gamepad Controls
Automatic Animation

The Meixner process is a four-parameter Lévy process that originated in the study of orthogonal polynomials and has been shown to be able to reproduce stock returns on several major exchanges with remarkable accuracy. In this Demonstration we test this fact for the S&P 500 index, following results described in [2]. We obtained the date for S&P 500 using the Mathematica function FinancialData. We used the Mathematica function SmoothKernelDistribution to obtain a smooth density function approximating the distribution of the data. We then compared the distribution thus obtained with the Meixner distribution using Shoutens' parameters. This confirmed that the Meixner distribution does indeed provide an excellent fit to the data. We then again used the function FinancialData to obtain S&P 500 index prices for the following decade. Although the new fit was somewhat worse, we found that by manipulating the parameters by hand, using Mathematica's dynamic functionality we could quickly obtain a better fit. We used the distance in variation (the integral of the absolute value of the difference between densities) as a measure of the goodness of fit, as Mathematica is able to compute it remarkably quickly. The value obtained by hand is included as a bookmark with the name "better fit". Finally, using this value as a starting value and applying the function NMinimize to the distance in variation, we were able to find a fit to the data for the 2001–2010 period that is almost as good as the one obtained by Schoutens for the earlier one.

References

[1] W. Schoutens, "The Meixner Process in Finance," EURANDOM Report, 2001(002), 2001 pp. 1–22.

[2] W. Schoutens, Lévy Processes in Finance, New York: John Wiley & Sons, 2003.

Andrzej Kozlowski

"Fitting the Meixner Distribution to S&P 500 Returns"
http://demonstrations.wolfram.com/FittingTheMeixnerDistributionToSP500Returns/
Wolfram Demonstrations Project
Published: January 18, 2012