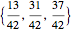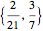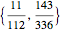Flowsnake Q-Function

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
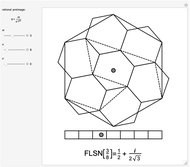
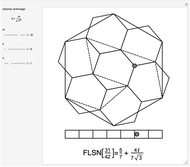
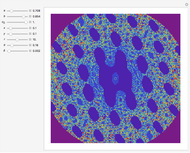
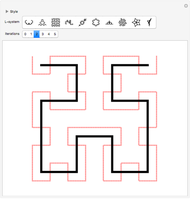
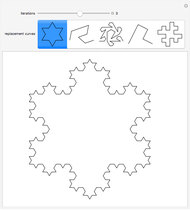
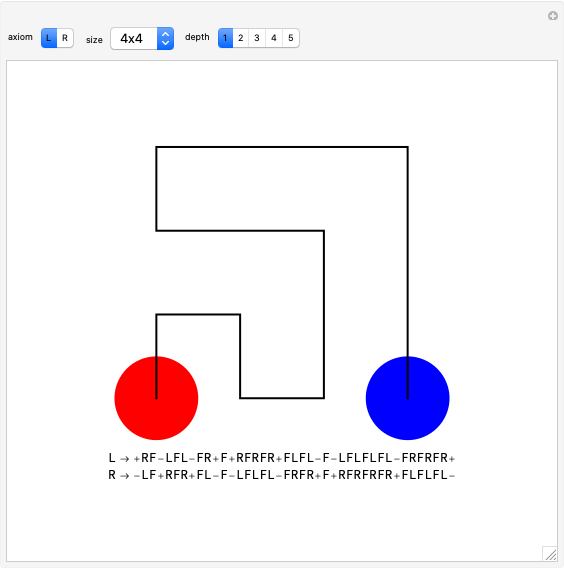
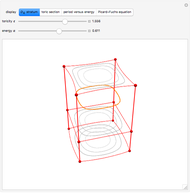
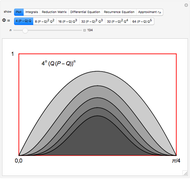
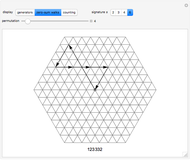
The flowsnake (also called a Gosper curve) is a space-filling curve, a surjection from 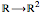 . The flowsnake
. The flowsnake  -function, a surjection
-function, a surjection 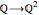 , determines a complex value,
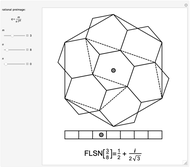
, determines a complex value, 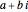 , for points along the curve with preimages that belong to the restricted domain. All valid preimages can be written in the form
, for points along the curve with preimages that belong to the restricted domain. All valid preimages can be written in the form 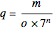 . When
. When  is an integer and
is an integer and 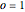 , the function values for the set of preimages
, the function values for the set of preimages 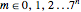 determine a traditional flowsnake interpolation. These points can be computed using a simple Lindenmayer system or a so-called
determine a traditional flowsnake interpolation. These points can be computed using a simple Lindenmayer system or a so-called  -function. Computation of other exact function values requires the
-function. Computation of other exact function values requires the  -function, provided here.
-function, provided here.
Contributed by: Brad Klee (September 2015)
Open content licensed under CC BY-NC-SA
Details
References
[1] M. Beeler, R. W. Gosper, and R. Schroeppel. "Item #115". HAKMEM MIT AI Memo 239. Feb. 29, 1972. Retyped and converted to html ('Web browser format) by Henry Baker, April, 1995. home.pipeline.com/~hbaker1/hakmem/topology.html#item115.
[2] B. Klee, "A Pit of Flowsnakes," Complex Systems, 24(4), 2015 pp. 275–294. doi:10.25088/ComplexSystems.24.4.275.
Snapshots
Permanent Citation