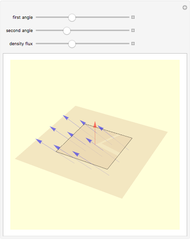
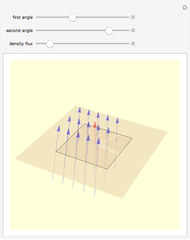
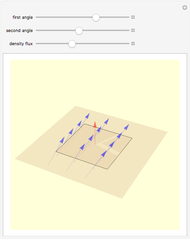
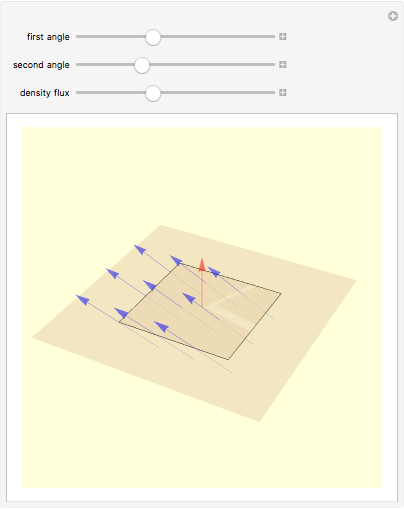
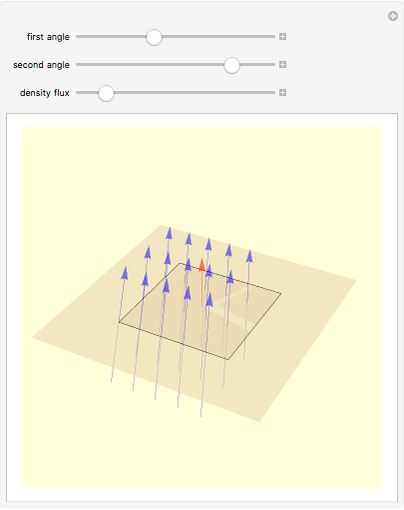
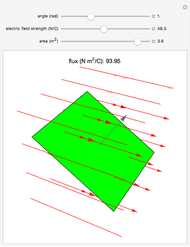
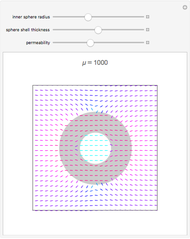
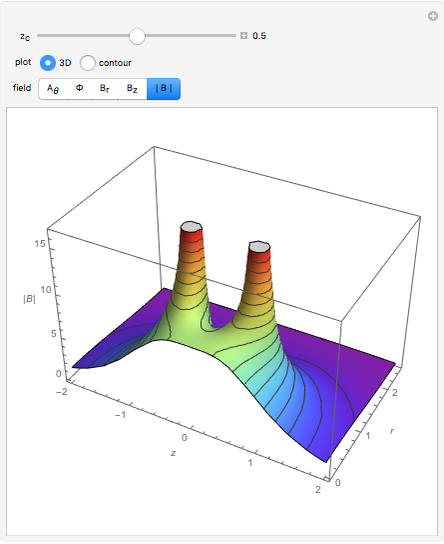
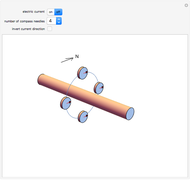
Consider an element of a smooth surface with a vector field passing through it. The strength of the field is proportional to the number of vectors passing through a given area. For a given strength, the flux density changes with the angle between the surface element and the field vectors. If the field is parallel to the surface, the flux is zero, while if the field is perpendicular to the surface, the flux is maximal.
In physics the most common applications appear in the study of electric and magnetic fields and in fluid dynamics.
Browse all topics
