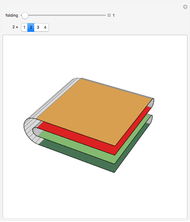
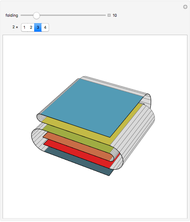
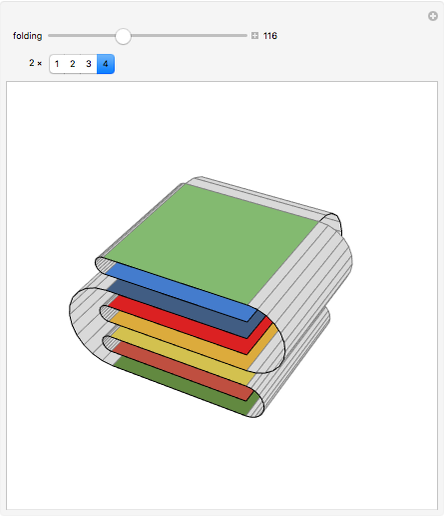
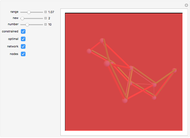
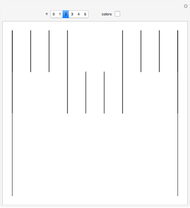
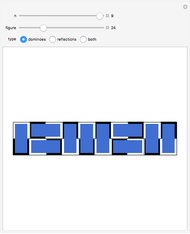
This Demonstration illustrates the different ways to fold a sheet of distinct stamps into a 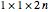stack. In each figure, the colored squares represent the stamps and the gray half-cylinders represent the perforation between adjacent stamps.
Snapshot 1: for a 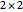sheet of stamps, all eight foldings have the same shape; it is clear that the number of foldings is less than , since two stamps initially diagonal from each other cannot be adjacent in the final stack
Snapshots 2, 3: for larger sheets, the counts are further diminished by rejecting foldings in which initial vertical or horizontal perforations would intersect
It is somewhat surprising that no general formula is known for counting the number of foldings of an sheet of stamps. The problem is sometimes called the map-folding problem.
M. Gardner, "The Combinatorics of Paper Folding," in Wheels, Life and Other Mathematical Amusements, New York: W. H. Freeman, 1983 pp. 60–61.
![[Snapshot]](HTMLImages/index.en/thumbnail_1.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_2.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_3.gif)
Embed Interactive Demonstration 
Browse all topics
