Folding a Net into an Octahedron Or Two Tetrahedra

Initializing live version

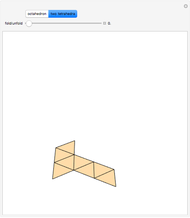
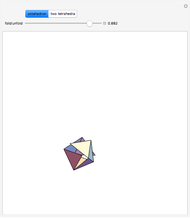
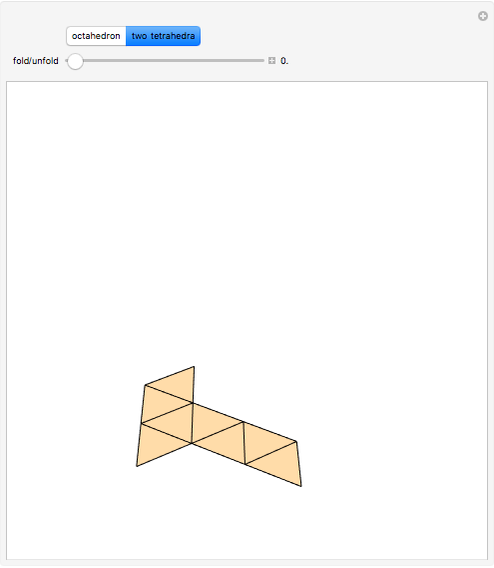
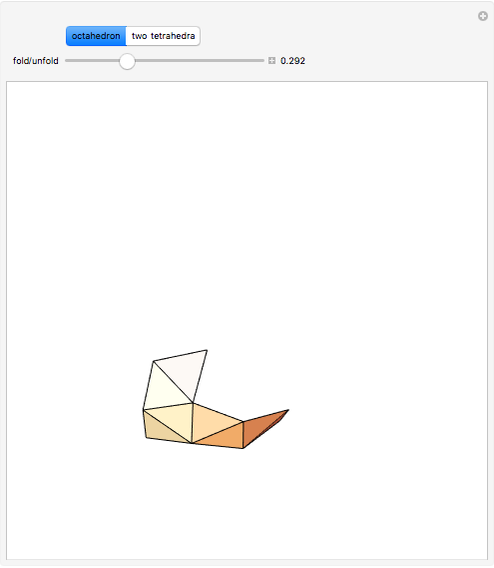
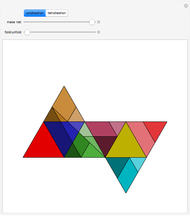
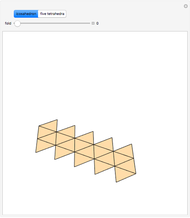
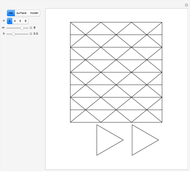
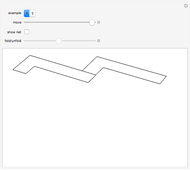
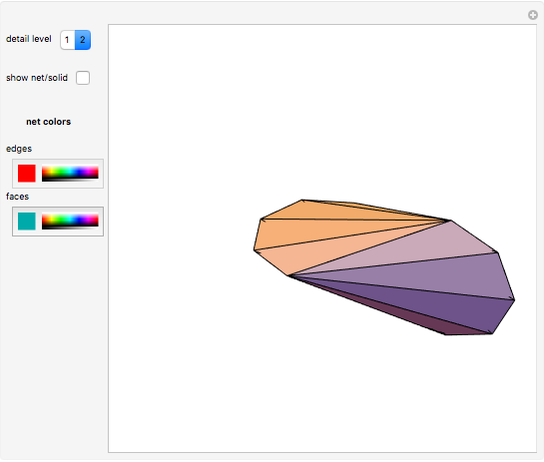
The Demonstration shows that the surface of a regular octahedron can be rearranged to form the surfaces of two regular tetrahedra.

Contributed by: Izidor Hafner (August 2013)
Open content licensed under CC BY-NC-SA

Snapshots

Reference

[1] G. N. Frederickson, Dissections: Plane & Fancy, New York: Cambridge University Press, 1997 p. 246. www.cs.purdue.edu/homes/gnf/book.html.


Feedback (field required)

Email (field required)	Name

Occupation	Organization

Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback. Send