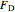Force Balances on a Truss

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
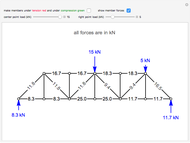
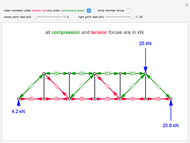
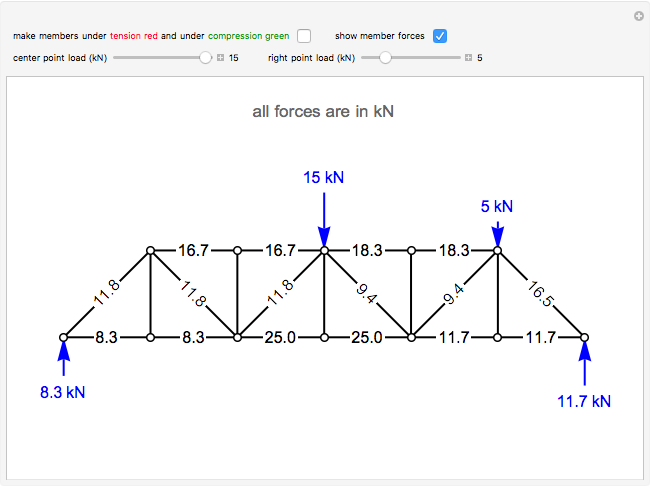
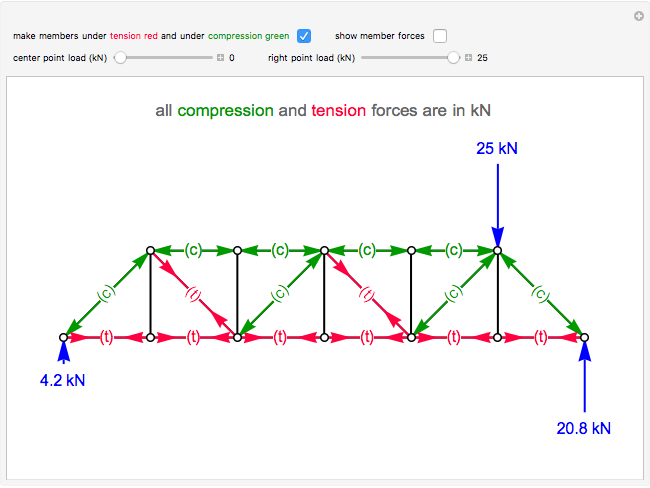
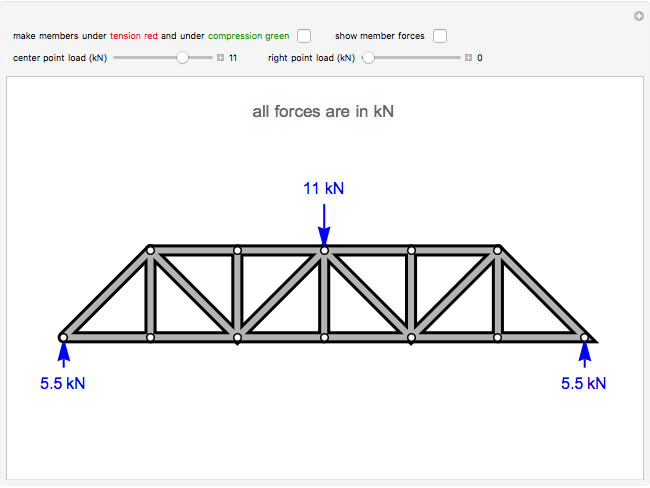
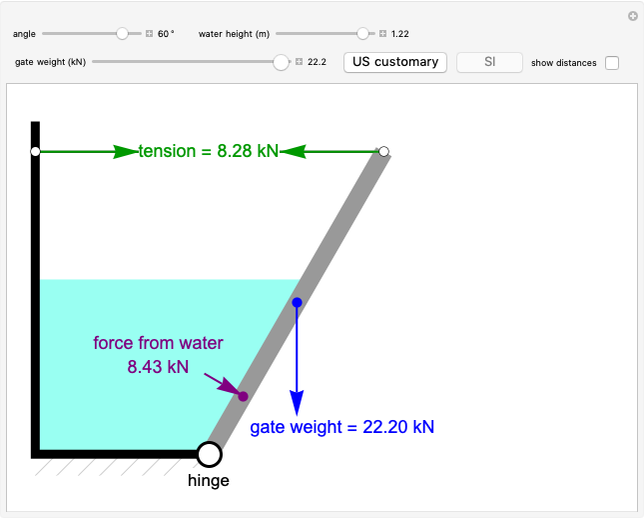
This Demonstration calculates the forces on the members of a planar truss.
[more]
Contributed by: Rachael L. Baumann (September 2017)
Additional contributions by: John L. Falconer
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA
Snapshots
Details
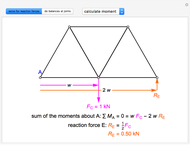
The method of joints is used to calculate the forces on each member of the truss. This is done by solving force balances around individual joints. First, calculate the reactions at the supports. Taking the sum of the moments at the left support:
 ,
,
where 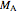 is the moment around support
is the moment around support 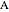 (left support),
(left support), 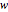 is the width of one member,
is the width of one member, 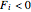 is the force applied to the joints at
is the force applied to the joints at 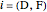 , and
, and  is the reaction at support
is the reaction at support  (right). The first two terms (
(right). The first two terms ( and
and  ) in the moment balance are positive because they would cause a clockwise rotation, and the third term (
) in the moment balance are positive because they would cause a clockwise rotation, and the third term (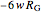 ) is negative because it would cause a counterclockwise rotation.
) is negative because it would cause a counterclockwise rotation.
Next, take the sum of the forces in the  direction to get
direction to get  :
:
 .
.
Begin solving for the forces of the members by doing force balances at the joints. The order of the balances around the joints listed here is the order in which they should be solved. Force balances are done assuming we can use logic to figure out which members are under tension and which are under compression. Starting at joint 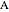 , there is a reaction force pushing up, so
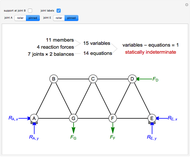
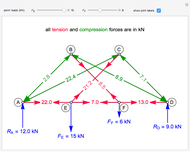
, there is a reaction force pushing up, so  must be pushing down (under compression). A labeled truss is shown in Figure 1.
must be pushing down (under compression). A labeled truss is shown in Figure 1.
Joint 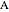
 ,
,
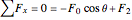 .
.
Joint 
 ,
,
 .
.
Joint 
 ,
,
 .
.
Joint 
 ,
,
 .
.
Joint 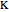
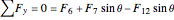 ,
,
 .
.
Joint 
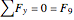 ,
,
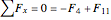 .
.
Joint 
 ,
,
 .
.
Joint 
 ,
,
 .
.
Joint 
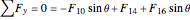 ,
,
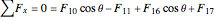 .
.
Joint 
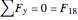 ,
,
 .
.
Joint 
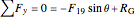 .
.
Note that all the vertical members are zero members, which means they are neither under tension nor under compression (force is 0 kN).

Figure 1.
Reference
[1] SkyCiv Cloud Engineering Software. "Tutorial to Solve Truss by Method of Sections." (Aug 29, 2017) skyciv.com/tutorials/tutorial-to-solve-truss-by-method-of-sections.
Permanent Citation