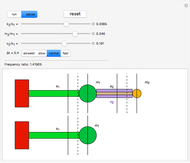
Forces on a Partially Submerged Gate

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
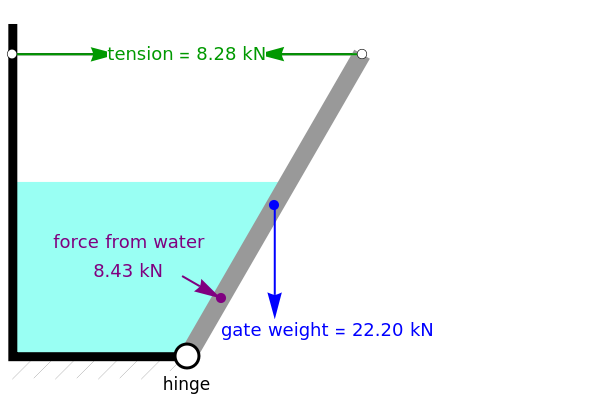
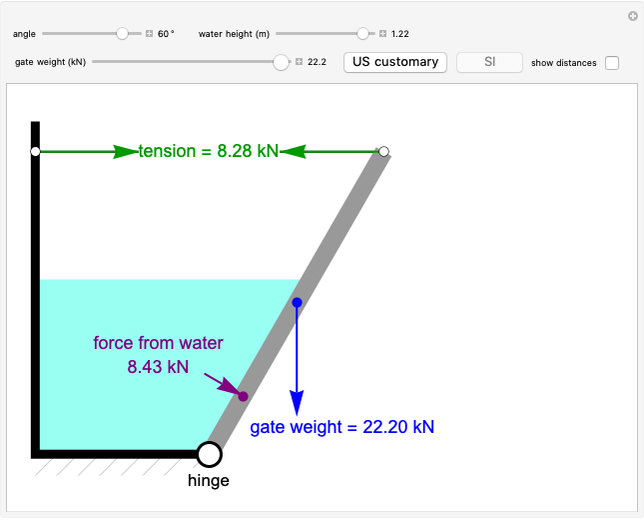
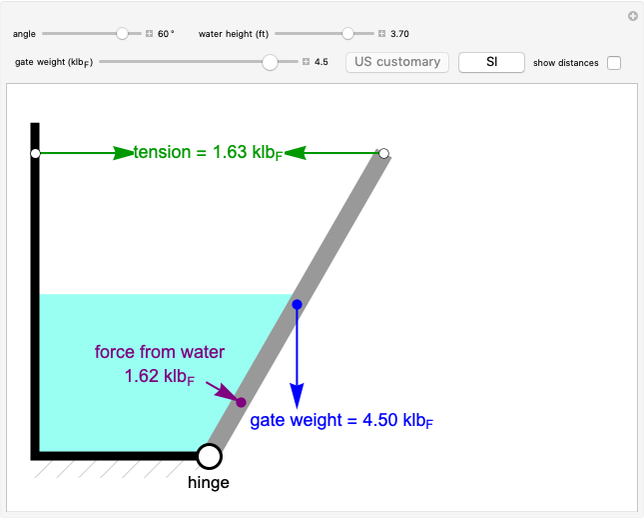
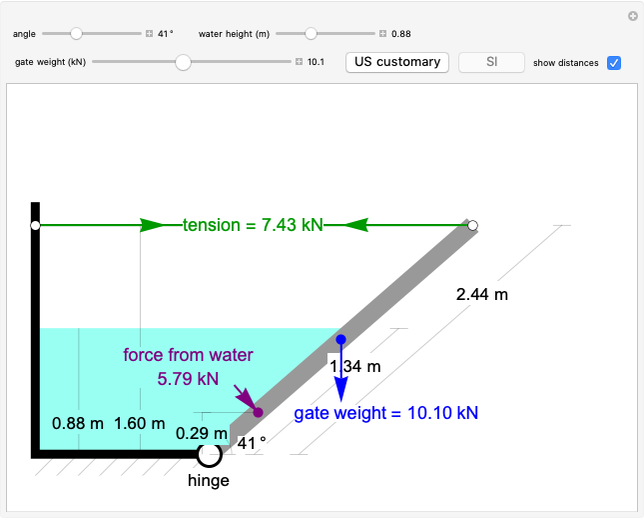
A gate, which is hinged at the bottom, is partially submerged under water, and a cable holds the gate closed. Use the sliders to set the angle of the gate, the weight of the gate, and the water height. Use the buttons to change the units from  and ft (US customary units) to kN and m (SI units). Check the "show distance" box to display distances. The Demonstration displays the cable tension needed to support the gate. When the tension is too high (greater than 4.23
and ft (US customary units) to kN and m (SI units). Check the "show distance" box to display distances. The Demonstration displays the cable tension needed to support the gate. When the tension is too high (greater than 4.23 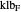 or 18.82 kN), the cable breaks.
or 18.82 kN), the cable breaks.
Contributed by: Rachael L. Baumann (November 2017)
Additional contributions by: John L. Falconer, Kimberly R. Bourland, and Neil Hendren
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This Demonstration determines the cable tension necessary to support a gate submerged under water (see Figure 1). The gate is 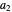 meters long, and the distance from the hinge to top of the water along the gate is
meters long, and the distance from the hinge to top of the water along the gate is 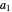 meters.
meters.
The magnitude of the resultant force due to the water is found by summing the differential forces 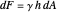 over the entire surface:
over the entire surface:
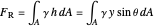 ,
,
where 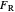 is the resultant force (N),
is the resultant force (N),  is the specific weight of water (
is the specific weight of water (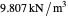 ),
), 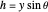 is the vertical distance from the top of the water to any point in the water (m),
is the vertical distance from the top of the water to any point in the water (m), 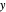 is the corresponding distance along the gate (m),
is the corresponding distance along the gate (m),  is the angle of the gate (degrees),
is the angle of the gate (degrees), 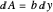 is differential area of the gate (
is differential area of the gate (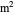 ), and
), and  is the width of the gate (m). Note that the specific weight
is the width of the gate (m). Note that the specific weight 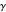 is the specific gravity
is the specific gravity  times the acceleration of gravity
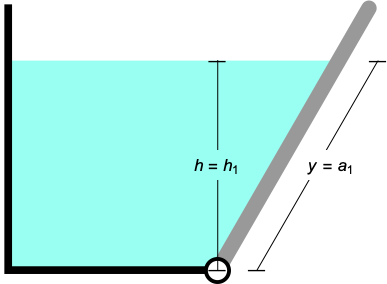
times the acceleration of gravity  . The total area of the gate that is in contact with water is
. The total area of the gate that is in contact with water is 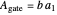 . This integral is from
. This integral is from 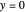 at the top of the water level to
at the top of the water level to 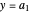 at the hinge.
at the hinge.
Since 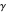 is constant, and for a fixed value of
is constant, and for a fixed value of  , the resultant force becomes:
, the resultant force becomes:
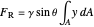 .
.
The integral  is:
is:
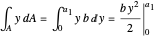 ,
,
this is then equal to:
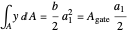 ,
,
the resultant force is then:
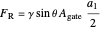 .
.
The sum of the moments around the hinge is equal to the moment of the resultant force at the  coordinate
coordinate 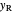 . Note that moment is proportional to the distance from the hinge to location of the force:
. Note that moment is proportional to the distance from the hinge to location of the force:
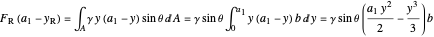 ,
,
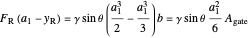 ,
,
and since 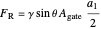 ,
,
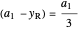 .
.
That is, the resultant force is located 1/3 of the distance from the hinge to the water level along the gate. A moment balance determines the tension  (kN) in the cable that is holding up the gate:
(kN) in the cable that is holding up the gate:
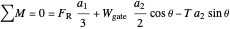 .
.
where 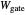 is the weight of the gate, which is located at the center of the gate. The tension is then:
is the weight of the gate, which is located at the center of the gate. The tension is then:
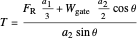 .
.
Figure 1
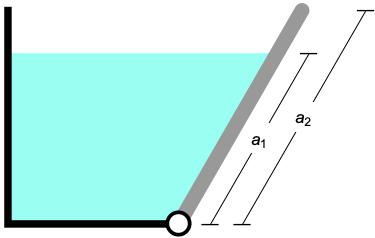
Figure 2
Reference
[1] B. R. Munson, T. H. Okiishi and W. W. Huebsch, Fundamentals of Fluid Mechanics, 6th ed., Hoboken, NJ: John Wiley & Sons, 2009 pp. 57–60.
Permanent Citation