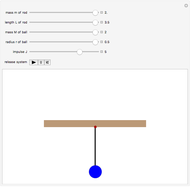
Forces on a Pendulum

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
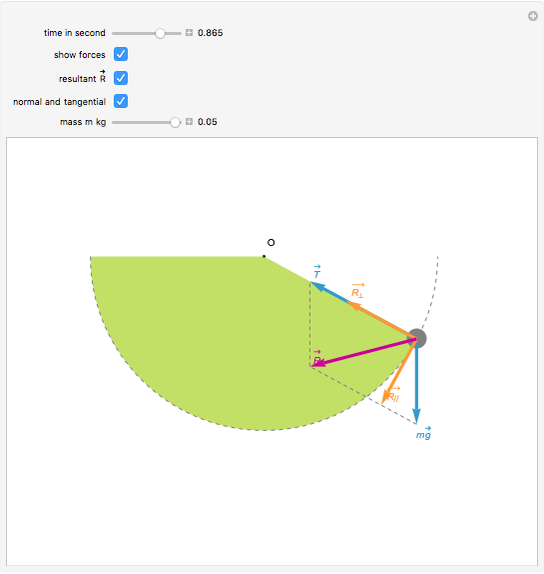
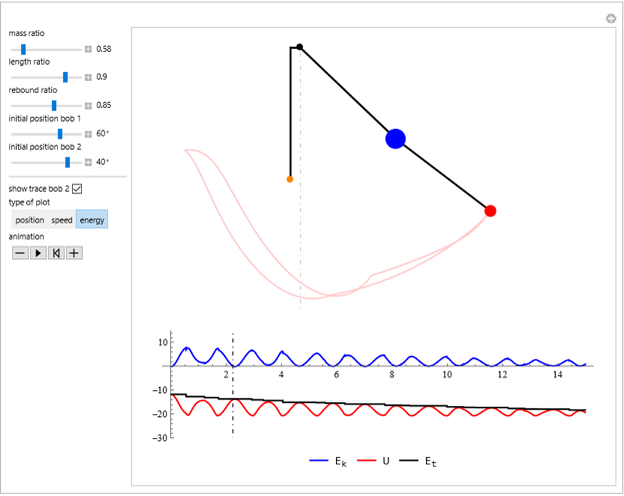
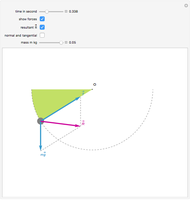
The simple pendulum is presented in all introductory physics textbooks. However, there are sometimes mistakes in the force diagrams for the motion of the pendulum perhaps due to a confusion regarding the correct relative magnitude of the forces acting on the swinging mass 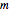 . Two forces act on this mass: the weight of the mass
. Two forces act on this mass: the weight of the mass 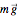 and the tension
and the tension 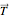 of the string, which is of variable magnitude. To compute the tension, we can consider the pendulum at any point and suppose it is not moving. Then the tension is equal to the normal component of the weight. If the angular velocity of the mass at this point is
of the string, which is of variable magnitude. To compute the tension, we can consider the pendulum at any point and suppose it is not moving. Then the tension is equal to the normal component of the weight. If the angular velocity of the mass at this point is  and if the mass describes an arc of a circle of radius
and if the mass describes an arc of a circle of radius 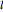 , it is subjected to a centripetal force given by
, it is subjected to a centripetal force given by 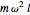 . The sum of these two forces gives the tension in the string; it is not tangent to the trajectory but rather points into the interior of the circular arc. This resultant can be decomposed into a centripetal force
. The sum of these two forces gives the tension in the string; it is not tangent to the trajectory but rather points into the interior of the circular arc. This resultant can be decomposed into a centripetal force  that corresponds to the curvature of the trajectory and a tangential force
that corresponds to the curvature of the trajectory and a tangential force  that determines the velocity of the mass.
that determines the velocity of the mass.
Contributed by: Bernard Vuilleumier (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
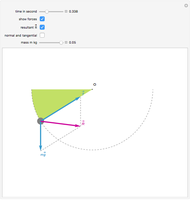
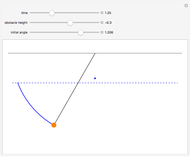
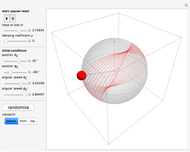
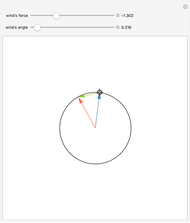
Snapshot 1: the pendulum is attached to O by a string and oscillates; two forces act on this pendulum, the weight of the mass 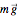 and the tension
and the tension 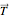 exercised by the string
exercised by the string
Snapshot 2: in general, the resultant 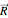 of theses two forces is not tangent to the trajectory; it points to the interior of the circle
of theses two forces is not tangent to the trajectory; it points to the interior of the circle
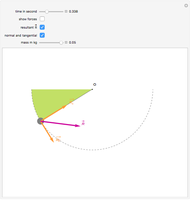
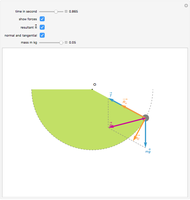
Snapshot 3: this resultant 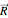 can be decomposed into a centripetal force
can be decomposed into a centripetal force 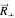 that corresponds to the curvature of the trajectory and a tangential force
that corresponds to the curvature of the trajectory and a tangential force 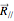 that determines the velocity of the mass
that determines the velocity of the mass
Analysis of the force and acceleration components in a two-dimensional pendulum has been the source of some confusion in the literature. Stan Wagon suggested the following summary of the problem: http://agm.cat/recerca-divulgacio/pendulum-TPT.pdf.
Permanent Citation