Four-Color Outer Median Cellular Automata on Graphs

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
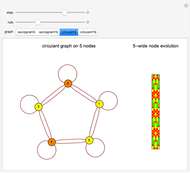
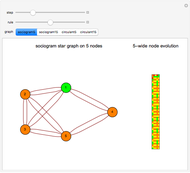
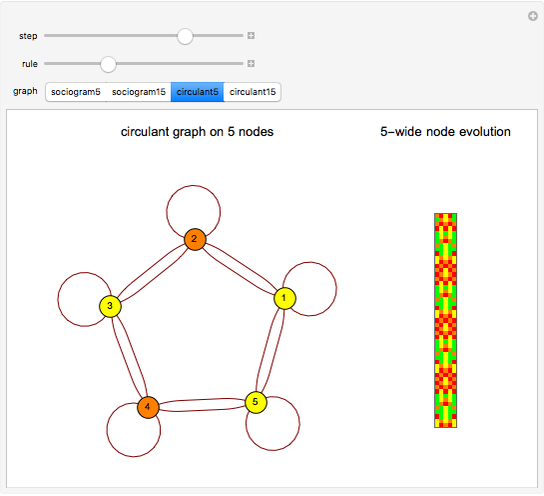
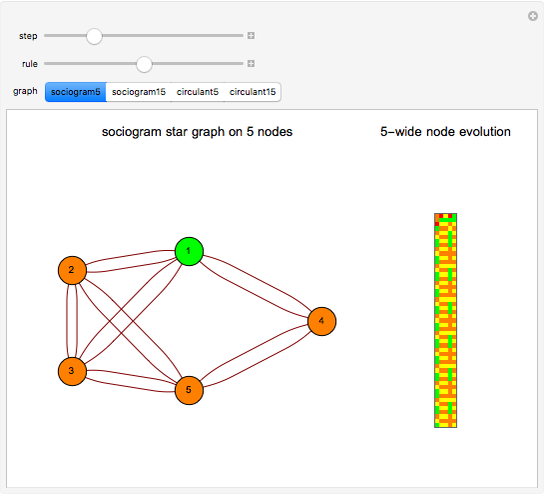
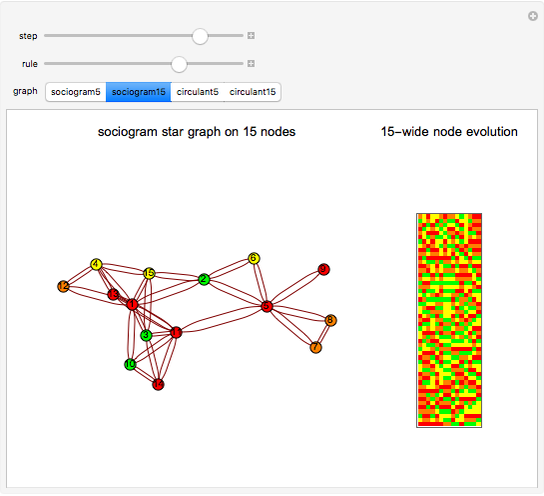
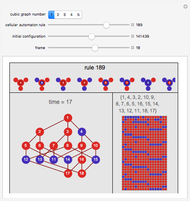
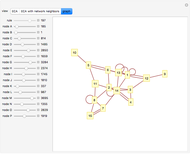
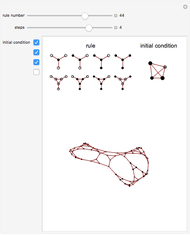
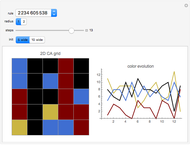
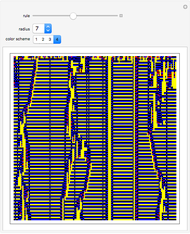
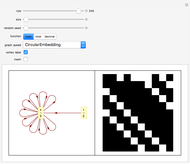
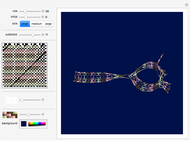
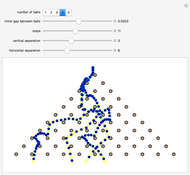
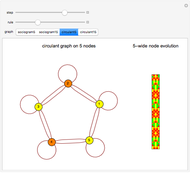
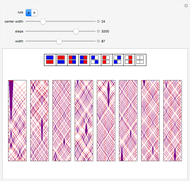
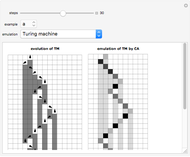
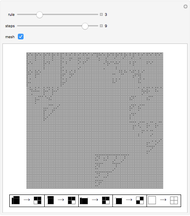
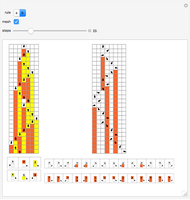
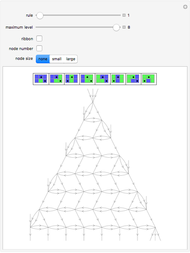
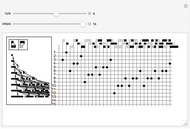
Outer median (OM) rules on cellular automata (CA) calculate the color of the next step of the active cell by looking at the neighbors of the active cell and taking the floor of the median of the colors of those neighbors. Then basic rules are applied on the resultant pairs: {active cell, floor of median of neighbors}. This effectively allows CA rules to be taken "off the lattice", whereby an active cell can have any number of neighbors and still have the same number of rules. Therefore, the CA translates naturally to application on a network of nodes (graph), each node representing an active cell, and the node neighbors representing the neighbors of the active cell. The node evolution is shown as an array plot, for 50 steps.
Contributed by: Abigail Nussey (July 2008)
Open content licensed under CC BY-NC-SA
Snapshots
Details
A set of 11 interesting four-color rules was provided for this Demonstration: {835410659, 165886556, 2586168012, 1853213473, 625101555, 793262014, 1215618935, 582466131, 2234605538, 31963262, 2751474038}
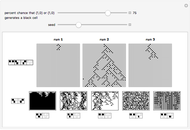
A sociogram is a graph that tries to emulate a social interaction network. These sociograms were built (by hand) to look like typical social networks such as those for Facebook friends or virus transmittal studies. A symmetric circulant graph was specifically chosen to compare against the irregular sociogram to illustrate the effects of these topological differences on the node evolutions. It is interesting to see that even with a symmetric circulant graph there is complex behavior, with the same rules sometimes producing complex, though different, behavior on different graphs with the same number of nodes.
You can also observe increasing likelihood of complexity with more nodes, though that is expected.
In the future, the author will be looking at outer median rules on graphs with respect to real-world models (mainly social interaction networks), perturbing the OM-ruled graphs, looking at "mass media"-like global neighbors, and so forth. The simplicity of the OM-ruled graphs is their power: they give one the ability to rework old-standard "Game of Life" models, inherently local or nonlocal only with very complex constraints, into something more naturally nonlocal.
This Demonstration was created as part of a project for the NKS Summer School 2008 (NKS|Online).
Permanent Citation
"Four-Color Outer Median Cellular Automata on Graphs"
http://demonstrations.wolfram.com/FourColorOuterMedianCellularAutomataOnGraphs/
Wolfram Demonstrations Project
Published: July 23 2008