Four Dividable Rhombohedra

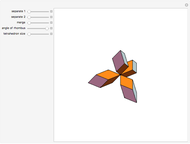
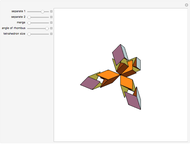
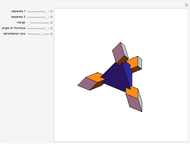
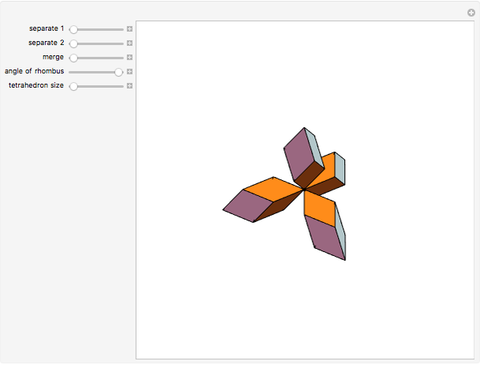
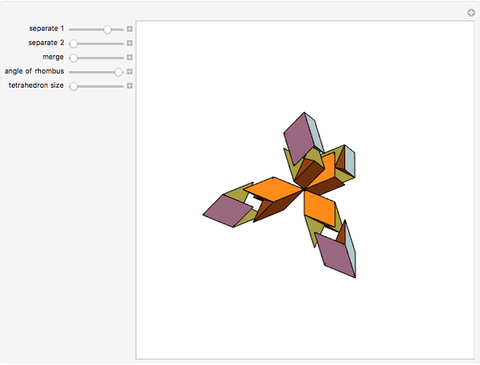
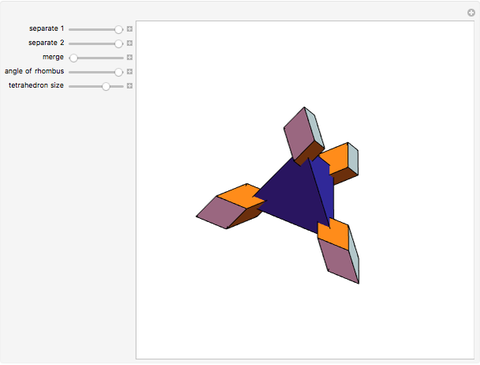
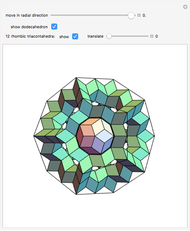
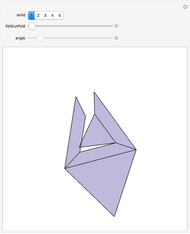
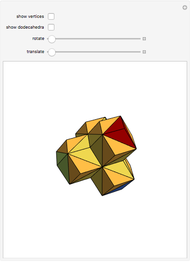
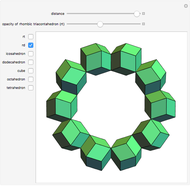
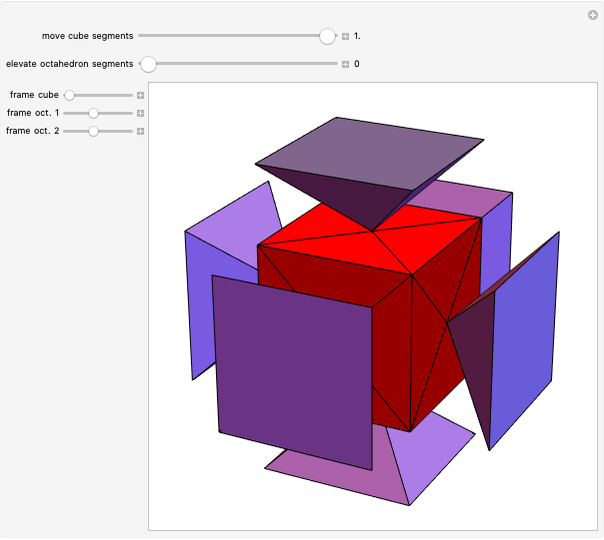
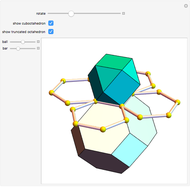
Four rhombohedra are placed within a tetrahedron so that each one has one of its vertices at the center of a tetrahedron and one of its vertices at a vertex of the tetrahedron. The rhombohedra can be divided into two equal parts along six triangles. When the diagonal ratio of the rhombus bordering the rhombohedron is 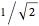, the four rhombohedra form a rhombic dodecahedron and the internal halves of the rhombohedra constitute a space-filling 24-faced polyhedra. When the ratio of the diagonals is 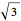, the four rhombohedra fit into the tetrahedron.