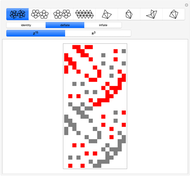
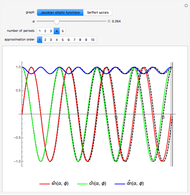
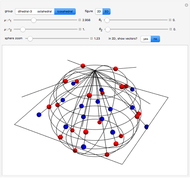
Four Hypergeometric Lattice Walks

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
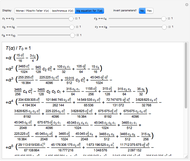
In a few special cases, Gauss's hypergeometric function 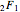 generates lattice walk counting sequences [1, 2]. Here we give four examples related to the elliptic integrals
generates lattice walk counting sequences [1, 2]. Here we give four examples related to the elliptic integrals 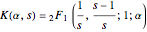 , with
, with 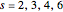 [3–6]. Up to rescaling (
[3–6]. Up to rescaling (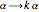 ) the
) the  expansion coefficient of
expansion coefficient of 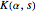 is the number of walks that return to the origin after
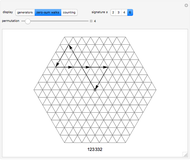
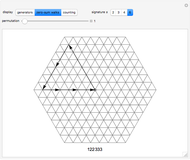
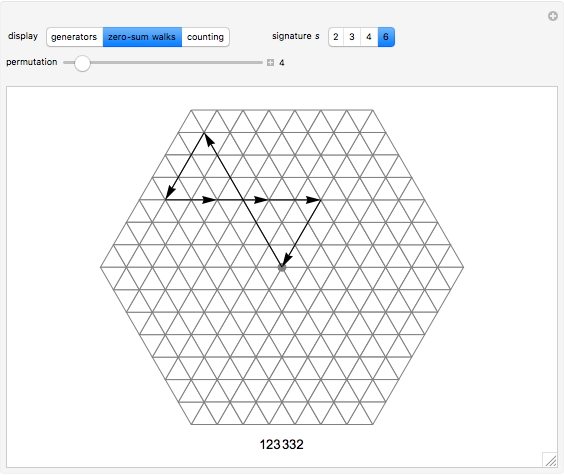
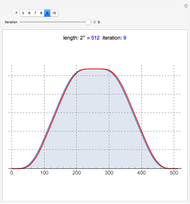
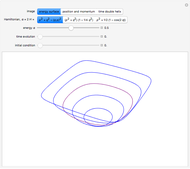
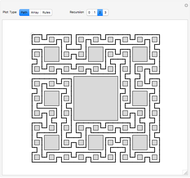
is the number of walks that return to the origin after 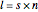 steps. This Demonstrations shows all valid walks when
steps. This Demonstrations shows all valid walks when  . Proof for higher
. Proof for higher  follows readily thereafter (see Details).
follows readily thereafter (see Details).
Contributed by: Brad Klee (August 2018)
Open content licensed under CC BY-NC-SA
Details
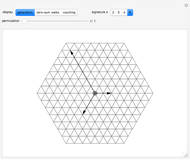
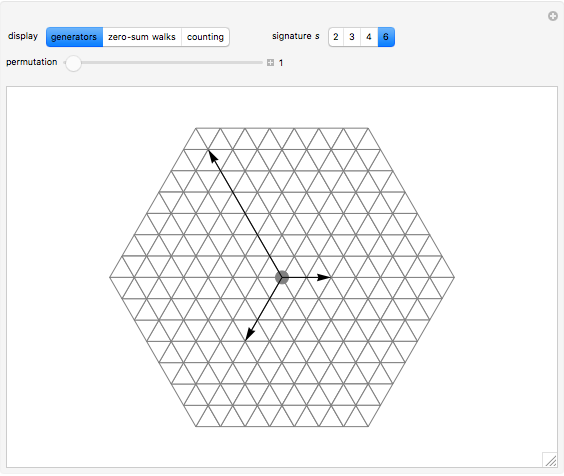
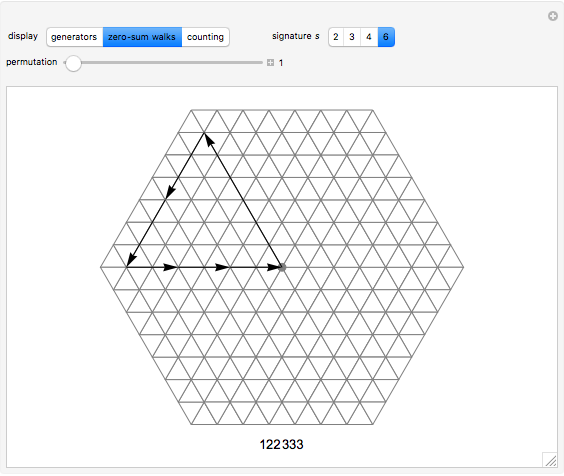
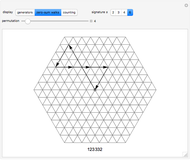
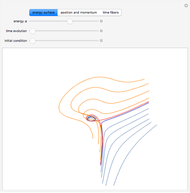
This Demonstration shows the generators of lattice walks with "display" set to "generators" and all loop walks with  with "display" set to "zero-sum walks". Each valid walk is associated to an
with "display" set to "zero-sum walks". Each valid walk is associated to an  -digit integer
-digit integer 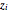 and to a vector zero sum. Thus the problem of counting valid paths reduces to a problem of counting distinct permutations of integers
and to a vector zero sum. Thus the problem of counting valid paths reduces to a problem of counting distinct permutations of integers 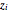 , which represent the coefficients of a vector zero sum.
, which represent the coefficients of a vector zero sum.
The case 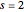 is more difficult than others because the set of walk-generating vectors contains four elements rather than three. The planar vector space is only of dimension two, implying two distinct zero sums,
is more difficult than others because the set of walk-generating vectors contains four elements rather than three. The planar vector space is only of dimension two, implying two distinct zero sums,
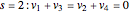 ,
,
which separate along the  and
and 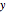 axes. All other valid zero sums are linear combinations of these fundamentals.
axes. All other valid zero sums are linear combinations of these fundamentals.
Clearly any loop walk has length 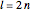 . If
. If 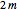 steps go along the
steps go along the  direction, then the total number of valid walks is given by [3, 6],
direction, then the total number of valid walks is given by [3, 6],
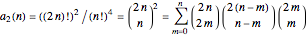 .
.
Such an identity appears in the original article [1], and nowadays is routinely proven using Zeilberger's algorithm [7, 8]. These numbers are generated as the coefficients of 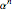 from the function
from the function
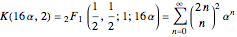 .
.
Cases with  are significantly easier to analyze. The set of walk-generating vectors contains only three elements, implying just one zero sum,
are significantly easier to analyze. The set of walk-generating vectors contains only three elements, implying just one zero sum,
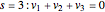 ,
,
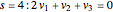 ,
,
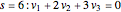 .
.
All other zero sums are simply multiples of these fundamentals. If a zero-sum walk exists, it must have length 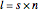 . In the analysis of length
. In the analysis of length 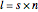 walks, we never encounter a binomial sum because any two
walks, we never encounter a binomial sum because any two 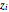 and
and 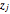 are related by permutation of digits.
are related by permutation of digits.
In general, coefficients 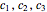 satisfy two constraints:
satisfy two constraints:
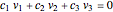 ,
,
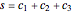 .
.
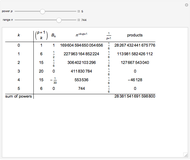
Considering all relevant permutation symmetries, the factorial function can be used to immediately write the counts:
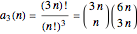 ,
,
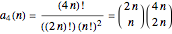 ,
,
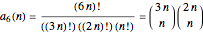 .
.
Again, these numbers are generated by hypergeometric functions: 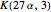 ,
, 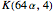 ,
, 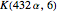 .
.
In fact, these three examples lead to a recipe for loop walks generated by three vectors. If the fundamental zero sum is of length 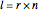 and
and 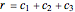 ,
,
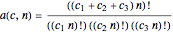 .
.
All such counting sequences have hypergeometric generating functions. For example, it is easy to find a generator geometry with 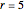 and
and  and
and 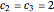 . Then counts of valid loop walks,
. Then counts of valid loop walks,
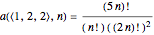 ,
,
are generated by [9]:
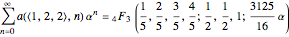 .
.
We do not know if this generating function has an interpretation in terms of algebraic plane curves, but it certainly is not an elliptic integral. This contrasts with the four special walks given in this Demonstration. Generating functions 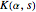 are also period-energy functions along families of elliptic plane curves.
are also period-energy functions along families of elliptic plane curves.
References
[1] G. Pólya, "Über eine Aufgabe der Wahrscheinlichkeitsrechnung betreffend die Irrfahrt im Straßennetz," Mathematische Annalen, 84, 1921 pp. 149–160. eudml.org/doc/158886.
[2] A. Bostan, "Calcul Formel pour la Combinatoire des Marches," Habilitation à Diriger des Recherches, Université Paris 13, 2017. specfun.inria.fr/bostan/HDR.pdf.
[3] N. J. A. Sloane. "A002894." The On-Line Encyclopedia of Integer Sequences. oeis.org/A002894.
[4] N. J. A. Sloane. "A006480." The On-Line Encyclopedia of Integer Sequences. oeis.org/A006480.
[5] N. J. A. Sloane. "A113424." The On-Line Encyclopedia of Integer Sequences. oeis.org/A113424.
[6] N. J. A. Sloane. "A000897." The On-Line Encyclopedia of Integer Sequences. oeis.org/A000897.
[7] N. J. A. Sloane. "A141902." The On-Line Encyclopedia of Integer Sequences. oeis.org/A141902.
[8] P. Paule and M. Schorn, "A Mathematica Version of Zeilberger’s Algorithm for Proving Binomial Coefficient Identities," Journal of Symbolic Computation, 20(5–6), 1995 pp. 673–698. doi:10.1006/jsco.1995.1071.
[9] N. J. A. Sloane. "A001459." The On-Line Encyclopedia of Integer Sequences. oeis.org/A001459.
Snapshots
Permanent Citation