Fourier Series Approximations to Roots of Unity

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
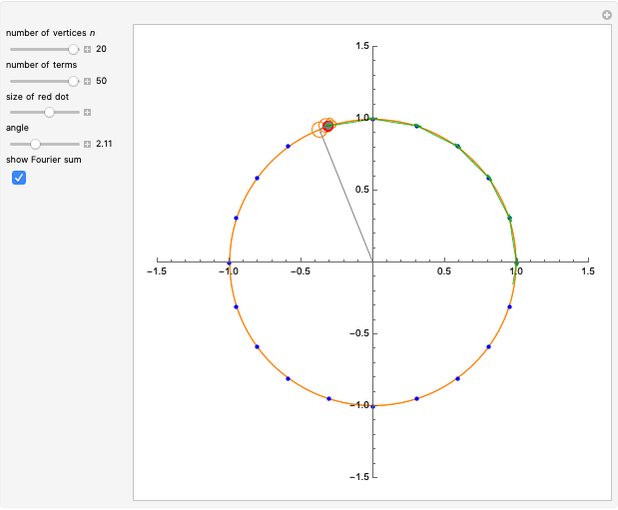
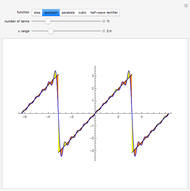
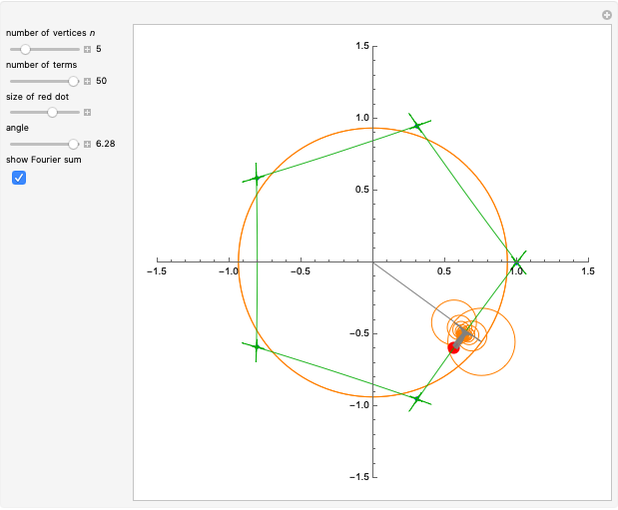
This Demonstration shows Fourier series approximations to functions representing the 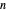 roots of unity, for
roots of unity, for 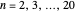 . The "number of vertices" is equal to
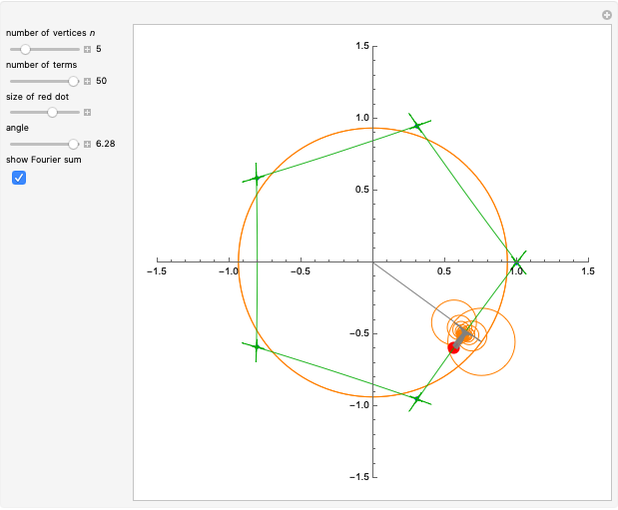
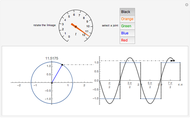
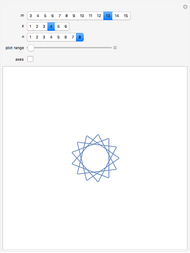
. The "number of vertices" is equal to 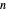 , with the roots of unity shown in blue. Each (gray) vector, representing the progressing Fourier series, is displayed along with the (orange) circle within which it rotates. The approximation is the point at the end of the final vector, indicated with a red dot. The "number of terms" equals the number of (gray) vectors/(orange) circles. You can select the angle that the vector from the origin makes with the ray
, with the roots of unity shown in blue. Each (gray) vector, representing the progressing Fourier series, is displayed along with the (orange) circle within which it rotates. The approximation is the point at the end of the final vector, indicated with a red dot. The "number of terms" equals the number of (gray) vectors/(orange) circles. You can select the angle that the vector from the origin makes with the ray 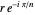 (
(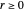 ) with the "angle" control. The checkbox lets you plot the partial Fourier sum (green), as the angle is swept from
) with the "angle" control. The checkbox lets you plot the partial Fourier sum (green), as the angle is swept from  to
to 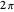 .
.
Contributed by: Walden Freedman (August 2022)
After work by: Grant Sanderson (3Blue1Brown)
Open content licensed under CC BY-NC-SA
Snapshots
Details
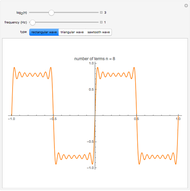
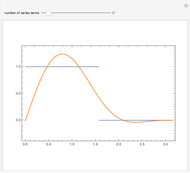
Let  be the
be the 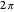 -periodic function defined by:
-periodic function defined by: 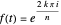 for
for 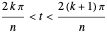 for
for 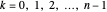 . It can be shown that the Fourier series for
. It can be shown that the Fourier series for  is given by
is given by
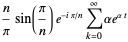
where 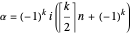 and
and  is the ceiling function. This Demonstration shows the partial sums with between one and 50 terms.
is the ceiling function. This Demonstration shows the partial sums with between one and 50 terms.
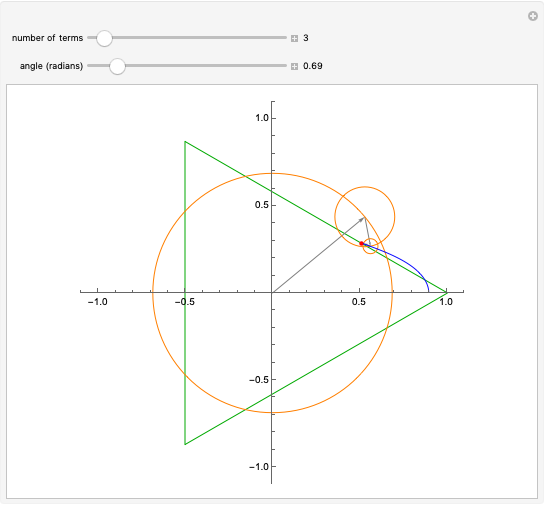
With a smaller number of vertices and terms, you can see how the circular motions combine. Try a slowed-down animation with a smaller number of vertices, say 2, 3 or 4, and 5, 6 or 7 terms. With more terms, the approximation improves in accuracy.
This Demonstration is inspired by the videos on Fourier Series by Grant Sanderson of 3Blue1Brown. There are other related animations online, such as: https://isaacvr.github.io/coding/fourier_transform.
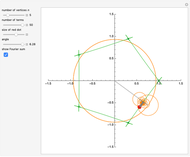
Snapshot 1: with 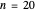 , we see that for large values of
, we see that for large values of 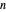 , the first term with
, the first term with 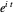 dominates and the green curve approximates the unit circle
dominates and the green curve approximates the unit circle
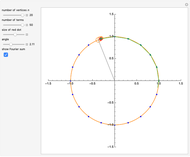
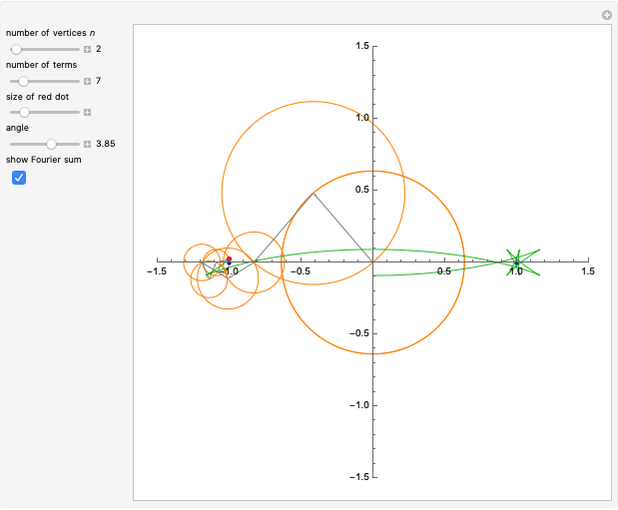
Snapshot 2: With 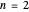 and an odd number of terms (7 in this case), we get an approximation between two "official" partial sums. The parametrization is not strictly real valued as it would be with an even number of terms; the number of vertices of the star-like figures one sees at
and an odd number of terms (7 in this case), we get an approximation between two "official" partial sums. The parametrization is not strictly real valued as it would be with an even number of terms; the number of vertices of the star-like figures one sees at 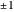 is equal to the odd number of terms.
is equal to the odd number of terms.
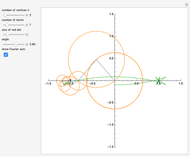
Snapshot 3: making the red dot larger can be helpful when viewing a large number of terms
Snapshot 4: viewing or animating slowly with a smaller number of terms and vertices can help one appreciate the mechanics of the motion
References
[1] E. M. Stein and R. Shakarchi, Fourier Analysis: An Introduction, Princeton, NJ: Princeton University Press, 2003.
[2] F. A. Farris, Creating Symmetry: The Artful Mathematics of Wallpaper Patterns, Princeton, NJ: Princeton University Press, 2015.
Permanent Citation