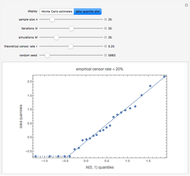
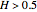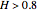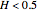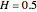Fractional Gaussian Noise

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
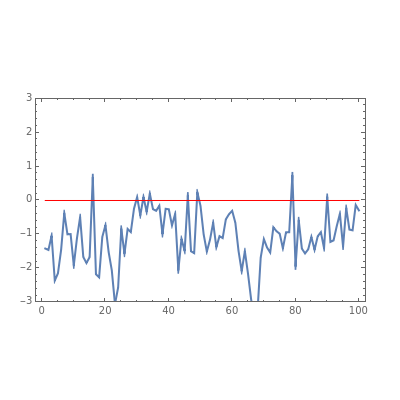
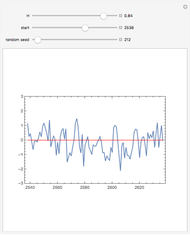
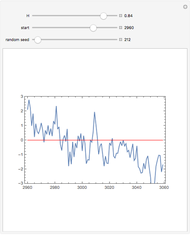
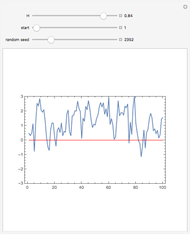
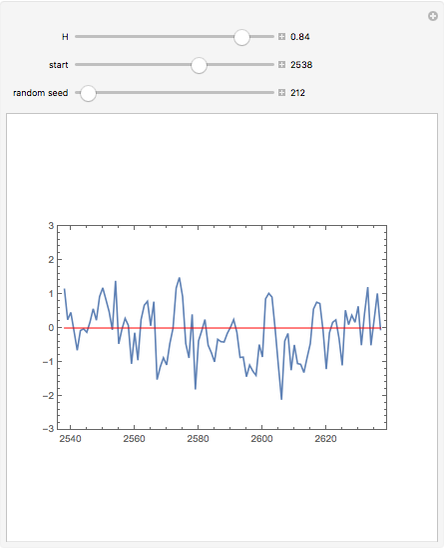
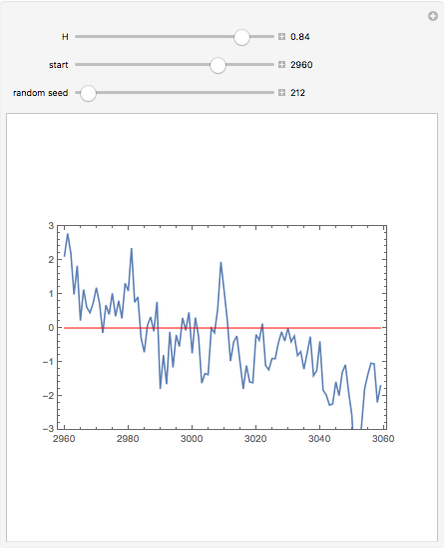
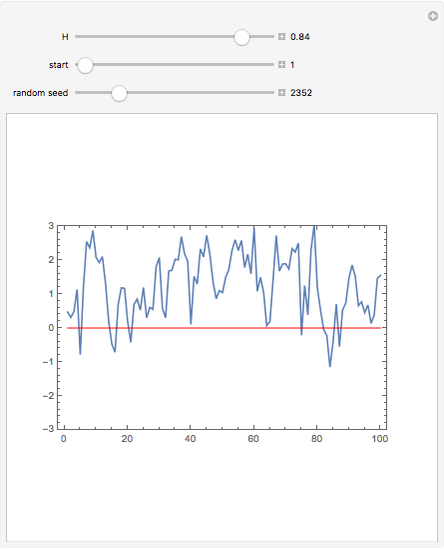
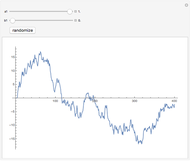
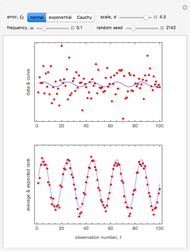
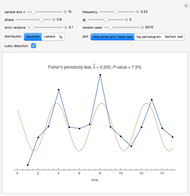
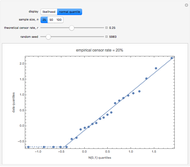
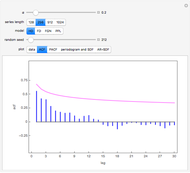
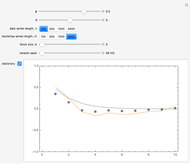
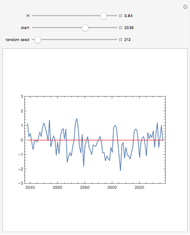
This Demonstration generates a fractional Gaussian noise time series of length 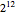 with Hurst coefficient
with Hurst coefficient 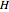 , mean 0, and variance 1. The plot shows 100 successive observations at a time. To avoid clutter, only the center is labeled on the horizontal bottom frame. By sliding the "start" bar, you can view successive subsequences.
, mean 0, and variance 1. The plot shows 100 successive observations at a time. To avoid clutter, only the center is labeled on the horizontal bottom frame. By sliding the "start" bar, you can view successive subsequences.
Contributed by: Ian McLeod (January 2012)
(University of Western Ontario)
Open content licensed under CC BY-NC-SA
Snapshots
Details
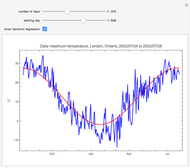
[1] provides a review of the fractional Gaussian noise and related long-memory time series models.
Reference
[1] K. W. Hipel and A. I. McLeod, Time Series Modelling of Water Resources and Environmental Systems, Amsterdam: Elsevier, 1994.
Permanent Citation