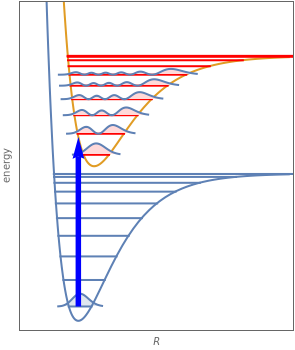
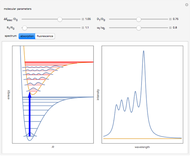
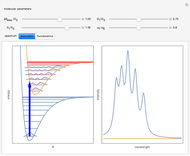
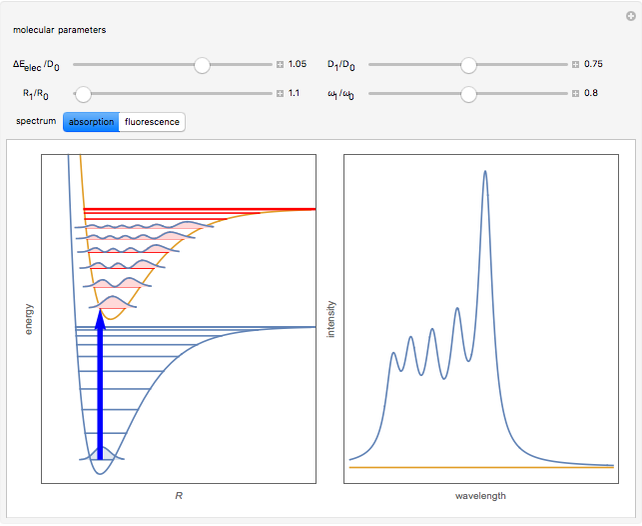
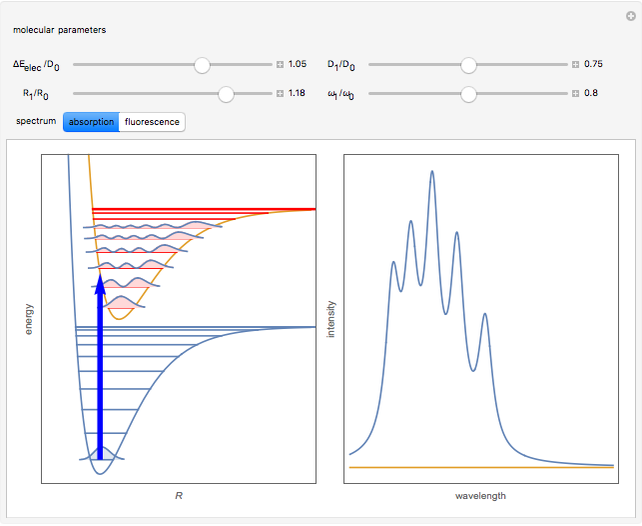
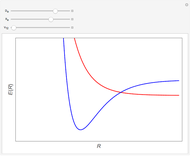
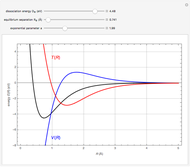
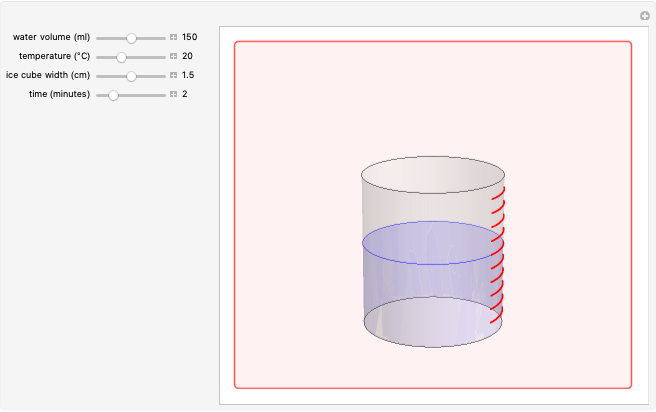
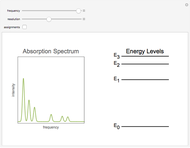
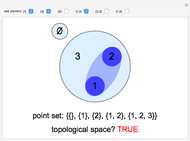
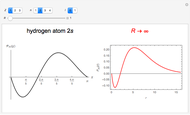
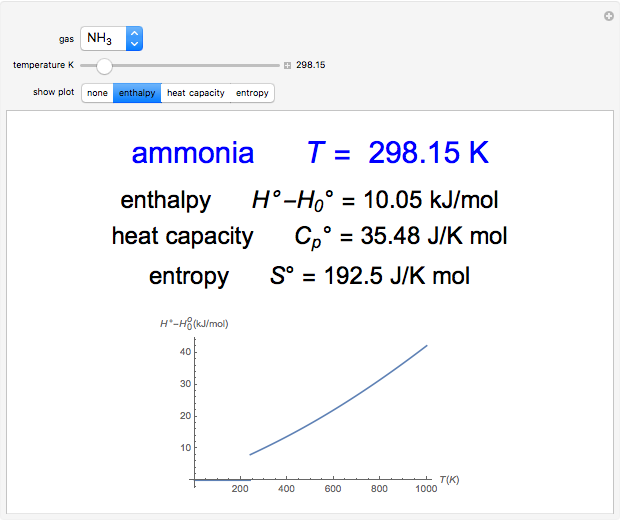
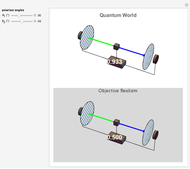
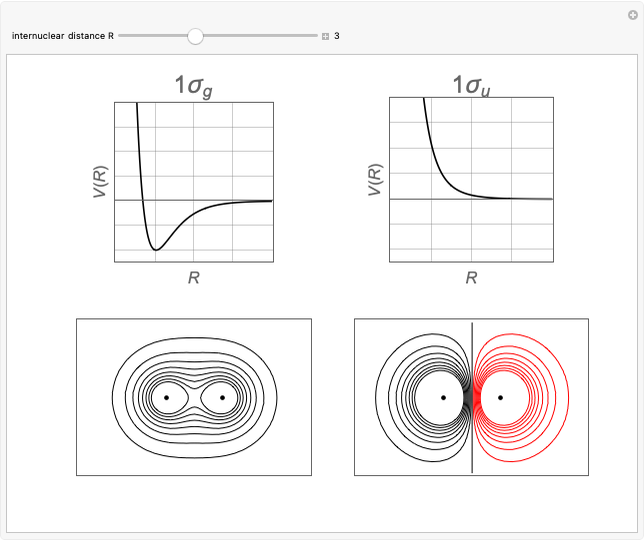
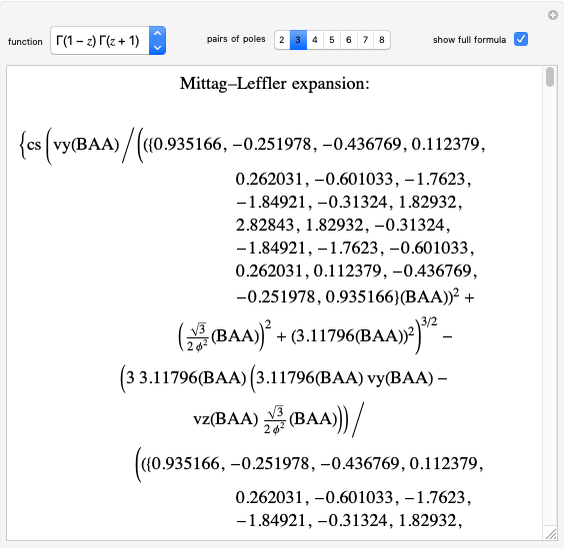
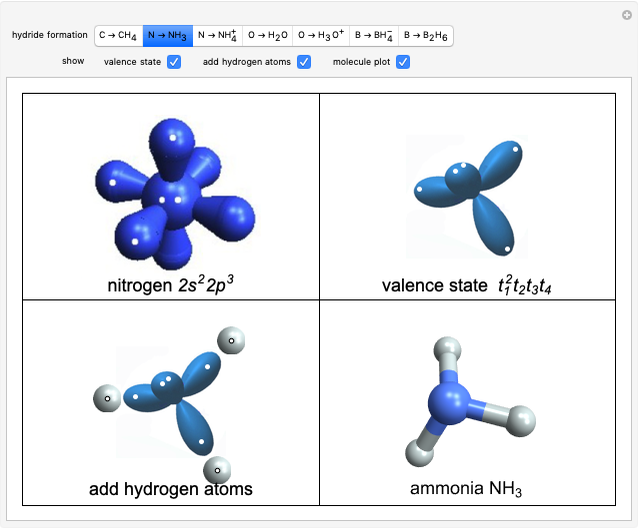
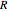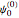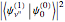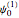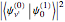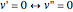When a diatomic molecule undergoes a transition to an excited electronic state higher by 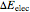 , it generally changes its vibrational and rotational quantum numbers as well. In the liquid state, the individual rotational levels are not generally resolved and the resulting process is characterized as a vibronic transition. Both the ground and excited electronic states are represented by potential energy curves, shown in blue and red, respectively, on the left-hand graphic. The probability densities of the first few ground state and excited-state vibrational levels,
, it generally changes its vibrational and rotational quantum numbers as well. In the liquid state, the individual rotational levels are not generally resolved and the resulting process is characterized as a vibronic transition. Both the ground and excited electronic states are represented by potential energy curves, shown in blue and red, respectively, on the left-hand graphic. The probability densities of the first few ground state and excited-state vibrational levels, 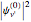 and
and 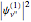 , are shown, superposed on the vibrational energy-level diagrams, with
, are shown, superposed on the vibrational energy-level diagrams, with 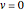 ,
, 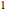 ,
,  , …. Here the superscripts refer to the electronic state, while the subscripts label the vibrational level.
, …. Here the superscripts refer to the electronic state, while the subscripts label the vibrational level.
[more]
At normal temperatures, only the 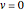 vibrational level of the ground state is occupied. When a molecule absorbs a photon in an electronic transition, the electrons can rearrange themselves much more rapidly than the much heavier nuclei (consistent with the Born–Oppenheimer approximation). Thus, electronic transition can be approximated by the vertical blue arrow to internuclear distances
vibrational level of the ground state is occupied. When a molecule absorbs a photon in an electronic transition, the electrons can rearrange themselves much more rapidly than the much heavier nuclei (consistent with the Born–Oppenheimer approximation). Thus, electronic transition can be approximated by the vertical blue arrow to internuclear distances 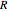 in the excited state very close to its maximum value in the ground state. This leads to a mixture of several excited-state vibrational levels, predominated by the level that overlaps maximally with the
in the excited state very close to its maximum value in the ground state. This leads to a mixture of several excited-state vibrational levels, predominated by the level that overlaps maximally with the 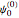 wavefunction. According to the Franck–Condon principle, the relative intensities of the individual vibrational peaks are proportional to the factors
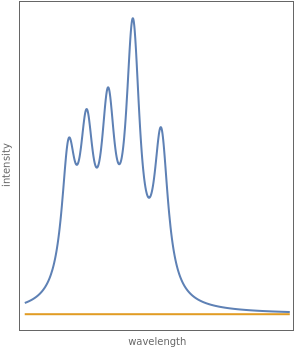
wavefunction. According to the Franck–Condon principle, the relative intensities of the individual vibrational peaks are proportional to the factors 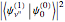 . This gives rise to an absorption spectrum shown in blue in the right-hand graphic. The relative intensity of the vibrational components depends on the molecular parameters of the two electronic states, but most sensitively on the difference between equilibrium internuclear distances,
. This gives rise to an absorption spectrum shown in blue in the right-hand graphic. The relative intensity of the vibrational components depends on the molecular parameters of the two electronic states, but most sensitively on the difference between equilibrium internuclear distances, 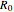 and
and 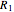 .
.
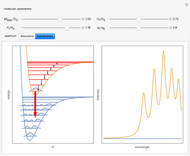
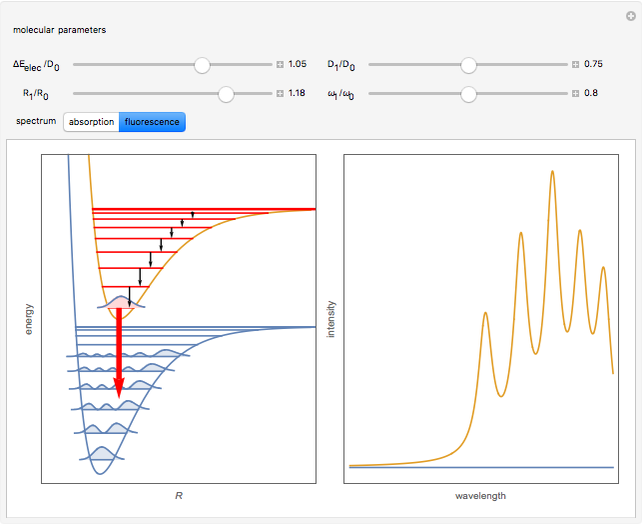
A molecule excited in an electronically allowed transition will generally return to its ground electronic state, a process called fluorescence, within the order of a few nanoseconds. Before it does so, most of the excited molecules will decay to the lowest vibrational state 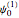 by radiationless transition processes (for example, molecular collisions). These are represented in the upper curve by a series of black arrows. Fluorescence will then produce a series of peaks corresponding to different vibrational levels of the ground state, with intensities proportional to the Franck–Condon factors
by radiationless transition processes (for example, molecular collisions). These are represented in the upper curve by a series of black arrows. Fluorescence will then produce a series of peaks corresponding to different vibrational levels of the ground state, with intensities proportional to the Franck–Condon factors 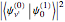 . Because of the geometry of the energy curves, the fluorescent spectrum is very nearly a mirror image of the absorption spectrum, with the transitions
. Because of the geometry of the energy curves, the fluorescent spectrum is very nearly a mirror image of the absorption spectrum, with the transitions 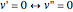 , meaning that this same transition occurs in both the absorption and fluorescence spectra. In this Demonstration, the Franck–Condon factors and spectral intensities are simulated since explicit computation would take too long.
, meaning that this same transition occurs in both the absorption and fluorescence spectra. In this Demonstration, the Franck–Condon factors and spectral intensities are simulated since explicit computation would take too long.
[less]
Details
Snapshot 1: the vibrational peaks in the absorption spectrum are notated, right to left, by 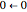 ,
, 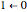 ,
, 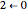 ,
, 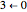 , etc.; the
, etc.; the 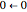 peak is dominant here since
peak is dominant here since 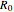 and
and 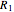 differ only slightly
differ only slightly
Snapshot 2: absorption spectrum with the 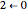 peak as the most intense
peak as the most intense
Snapshot 3: corresponding fluorescence spectrum; the peaks are notated, left to right, by 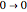 ,
, 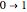 ,
, 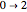 ,
, 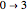 , etc.; note the near mirror image shapes of the absorption and fluorescence spectra
, etc.; note the near mirror image shapes of the absorption and fluorescence spectra
Reference
[1] S. M. Blinder, Introduction to Quantum Mechanics, Amsterdam: Elsevier, 2004 pp. 229–232.

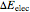 , it generally changes its vibrational and rotational quantum numbers as well. In the liquid state, the individual rotational levels are not generally resolved and the resulting process is characterized as a vibronic transition. Both the ground and excited electronic states are represented by potential energy curves, shown in blue and red, respectively, on the left-hand graphic. The probability densities of the first few ground state and excited-state vibrational levels,
, it generally changes its vibrational and rotational quantum numbers as well. In the liquid state, the individual rotational levels are not generally resolved and the resulting process is characterized as a vibronic transition. Both the ground and excited electronic states are represented by potential energy curves, shown in blue and red, respectively, on the left-hand graphic. The probability densities of the first few ground state and excited-state vibrational levels, 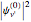 and
and 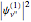 , are shown, superposed on the vibrational energy-level diagrams, with
, are shown, superposed on the vibrational energy-level diagrams, with 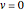 ,
, 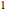 ,
,  , …. Here the superscripts refer to the electronic state, while the subscripts label the vibrational level.
, …. Here the superscripts refer to the electronic state, while the subscripts label the vibrational level.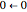 ,
, 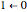 ,
, 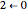 ,
, 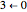 , etc.; the
, etc.; the 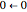 peak is dominant here since
peak is dominant here since 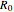 and
and 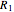 differ only slightly
differ only slightly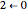 peak as the most intense
peak as the most intense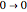 ,
, 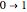 ,
, 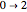 ,
,  , etc.; note the near mirror image shapes of the absorption and fluorescence spectra
, etc.; note the near mirror image shapes of the absorption and fluorescence spectra