Frictional Pressure Drop in a Pipe

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
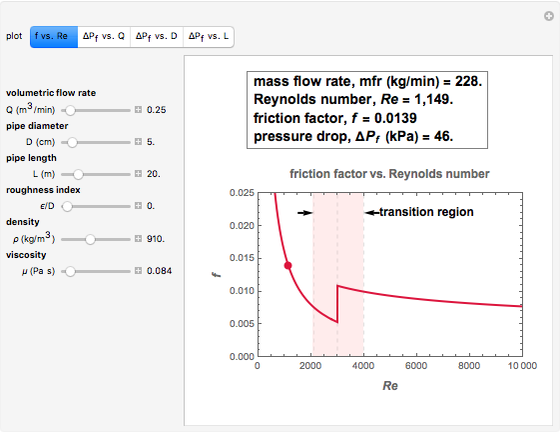
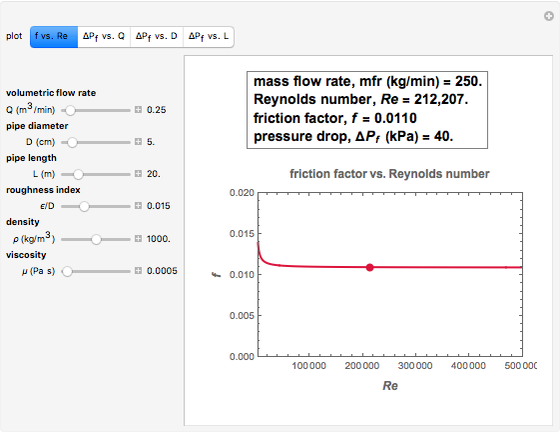
This Demonstration calculates and displays the pressure drop in a pipe due to friction as a function of the liquid's volumetric flow rate, the pipe's diameter, length, and degree of roughness, and the liquid's density and viscosity. It also calculates and displays the liquid's mass flow rate, the Reynolds number, and the corresponding friction factor. You can choose one of the following plots to display: the friction factor versus Reynolds number (Moody diagram) or the pressure drop versus the flow rate, the pipe's diameter, or its length.
Contributed by: Mark D. Normand and Micha Peleg (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
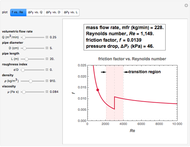
Snapshot 1: oil in a smooth pipe in laminar flow
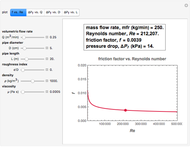
Snapshot 2: water in a smooth pipe in turbulent flow
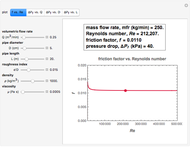
Snapshot 3: water in a rough pipe in turbulent flow
Snapshot 4: concentrated dextrin solution in a smooth pipe in turbulent flow
This Demonstration calculates the pressure of a liquid in a pipe, 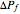 (in kPa), as a function of its volumetric flow rate,
(in kPa), as a function of its volumetric flow rate, 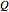 (in
(in 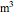 /min), the pipe's diameter,
/min), the pipe's diameter, 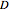 (in cm), length,
(in cm), length, 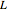 (in m), and degree of roughness,
(in m), and degree of roughness, 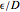 (dimensionless), and the liquid's density,
(dimensionless), and the liquid's density,  (in kg/
(in kg/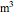 ), and viscosity,
), and viscosity,  (in Pa s). It also calculates and displays the liquid's mass flow rate,
(in Pa s). It also calculates and displays the liquid's mass flow rate,  (in kg/s), the Reynolds number,
(in kg/s), the Reynolds number, 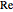 (dimensionless), and the friction factor,
(dimensionless), and the friction factor, 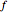 (dimensionless).
(dimensionless).
A Reynolds number of less than 2100 implies laminar flow, in which case, according to the Hagen–Poiseuille equation,  . A Reynolds number greater than 4000 implies turbulent flow, for which there are different ways to estimate the friction factor,
. A Reynolds number greater than 4000 implies turbulent flow, for which there are different ways to estimate the friction factor, 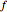 . The one used in this Demonstration, commensurate with the Moody diagram in the cited references, is based on the numerical solution of the equation
. The one used in this Demonstration, commensurate with the Moody diagram in the cited references, is based on the numerical solution of the equation 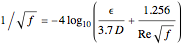 .
.
A transition from laminar to turbulent flow or vice versa occurs when 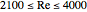 , in which case the use of either equation should be done with caution. This region is shaded in pink on the
, in which case the use of either equation should be done with caution. This region is shaded in pink on the 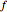 versus
versus 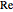 plot.
plot.
The displayed plot type is chosen with one of the following setters: 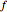 vs.
vs. 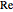 (the Moody diagram),
(the Moody diagram), 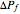 versus
versus 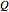 ,
, 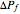 versus
versus 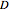 , or
, or 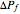 versus
versus 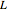 . Use the sliders to enter the current values of the parameters
. Use the sliders to enter the current values of the parameters 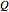 ,
, 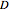 ,
, 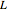 ,
, 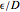 ,
,  , and
, and  . The conditions corresponding to the current settings of the parameters are marked as colored dots on the plots. The numerical values of
. The conditions corresponding to the current settings of the parameters are marked as colored dots on the plots. The numerical values of  ,
, 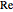 ,
, 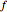 , and
, and 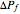 are displayed in a box above each plot.
are displayed in a box above each plot.
Note that the pipe's roughness only affects the friction factor in the turbulent regime.
To apply the Demonstration to pipe lengths greater than 100 m, simply scale a smaller result.
References:
D. W. Green and R. H. Perry, Perry's Chemical Engineer's Handbook, New York, NY: McGraw–Hill, 2008.
C. J. Geankoplis, Transport Processes and Unit Operations, 2nd ed., Boston: Allyn and Bacon, 1983.
Permanent Citation