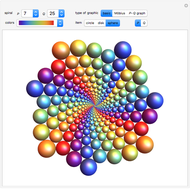
Gailiunas's Spiral Tilings

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
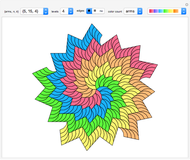
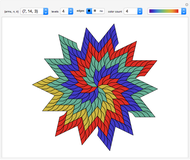
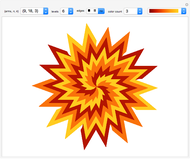
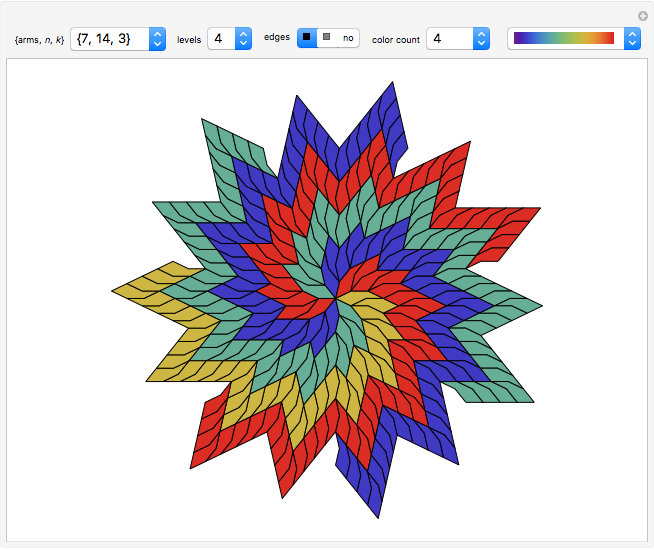
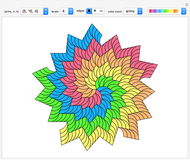
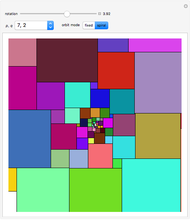
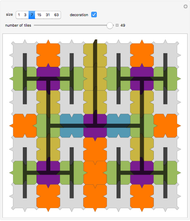
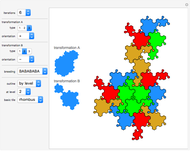
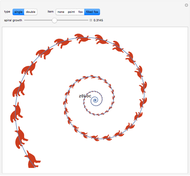
Explore a series of 52 spirals made from intersecting regular polygons with up to 36 vertices.
Contributed by: Dieter Steemann (September 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Paul Gailiunas [1] found a method that can produce spirals with three or more arms. This Demonstration shows 52 spirals made from intersecting  -gons up to
-gons up to 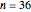 with all possible numbers of arms from 3 to 18. The basic polygonal tiles can be considered as bent wedges with three boundaries made of
with all possible numbers of arms from 3 to 18. The basic polygonal tiles can be considered as bent wedges with three boundaries made of  equal edges: a base of 1 segment, a convex side using
equal edges: a base of 1 segment, a convex side using  segments and a concave side using
segments and a concave side using  segments. For fewer arms, several spirals with the same number of arms originating from different
segments. For fewer arms, several spirals with the same number of arms originating from different  -gons are given.
-gons are given.
These monohedral spiral tilings are nonperiodic, have rotational symmetry and tile the plane.
Controls
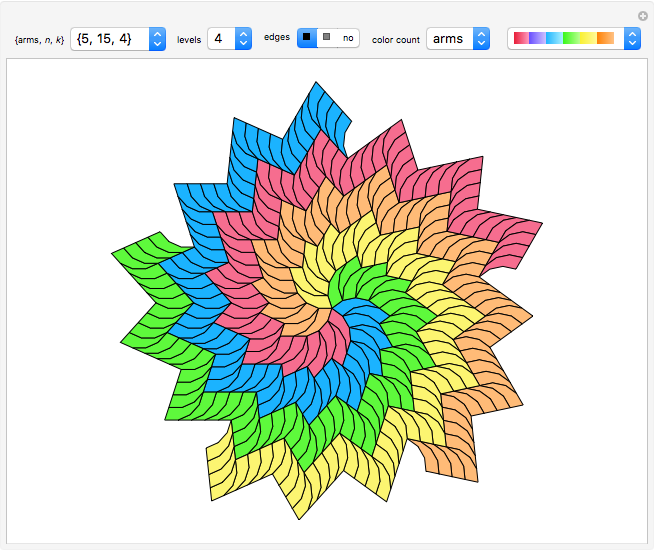
"arms,  ,
,  ": select one of the 52 spirals with the given number of arms, made from a specific
": select one of the 52 spirals with the given number of arms, made from a specific  -gon, using
-gon, using  segments at the convex side.
segments at the convex side.
"levels": controls the length of the arms.
"edges": use this checkbox for enhancing the boundaries of the polygons.
"color count": set the number of cyclic colors selected from the color palette popup menu. Selecting "arms" provides different colors for each arm.
Reference
[1] P. Gailiunas, "Spiral Tilings," in Bridges: Mathematical Connections in Art, Music, and Science, Winfield, KS: Bridges Conference, 2000 pp. 133–140. archive.bridgesmathart.org/2000/bridges2000-133.pdf.
Permanent Citation