Galileo's Paradox

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
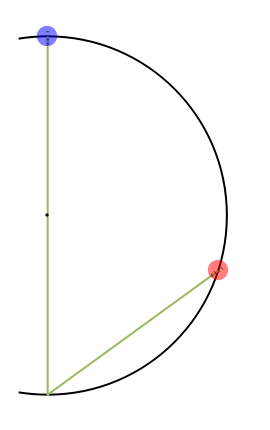
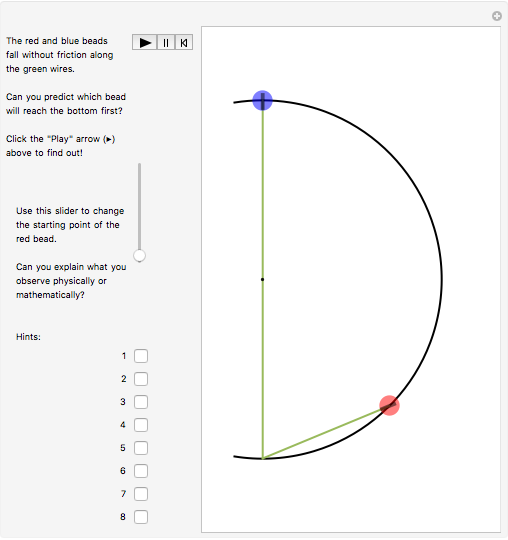
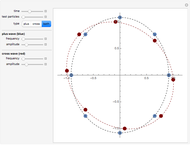
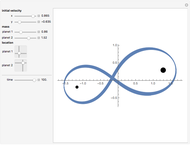
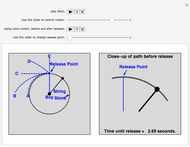
The blue bead falls straight down to the bottom of the circle along the vertical green wire.
[more]
Contributed by: Fernand Brunschwig (March 2011)
Open content licensed under CC BY-NC-SA
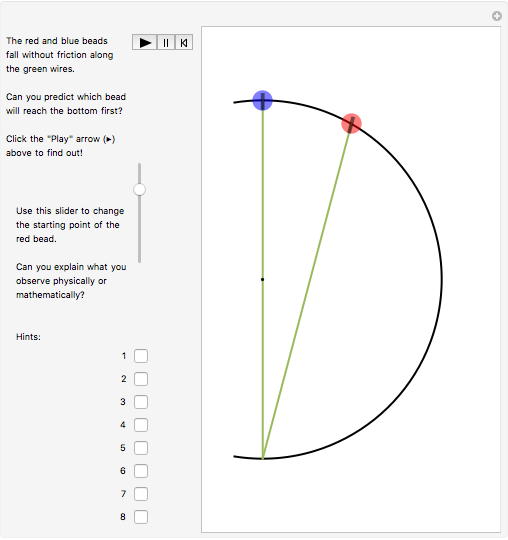
Snapshots
Details
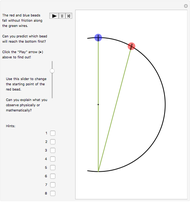
Falling objects seem familiar but their behavior can often be contrary to intuition. Here is a chance to see if you can predict the results of a "race" between two bodies falling along different paths towards the same point. Click the "Play" (right arrow ▶) button to start the race and find out! You can use the slider at the left to change the red ball's starting point. Does that change the outcome? Can you explain the results qualitatively? Can you calculate the times of descent for both balls and resolve Galileo's paradox? The snapshots show various starting positions for the red ball. This problem was first mentioned in 1602 by Galileo; see D. B. Meli, Thinking with Objects, Baltimore: Johns Hopkins University Press, 2006 p. 71.
Resolution of the paradox:
Both objects start from rest and are accelerated uniformly by gravity. Therefore the distances traveled (D and L), their accelerations 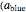 and
and 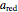 ), and the times elapsed
), and the times elapsed  and
and 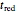 ) are related as follows:
) are related as follows:
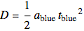 ,
,
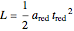 .
.
The blue bead accelerates at 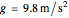 . Therefore,
. Therefore, 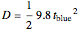 .
.
Solving for  yields:
yields:  .
.
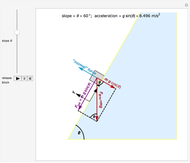
However, the red bead moves diagonally and its acceleration is, therefore, proportionally smaller. From the diagram, you can see that acceleration of the red bead will be the diagonal component of acceleration of the blue bead, that is, 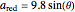 . Substituting into
. Substituting into 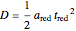 yields
yields
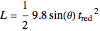 .
.
Finally, you can see from the diagram that 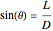 . Substituting this into the equation immediately above yields:
. Substituting this into the equation immediately above yields:
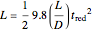 .
.
Solving for 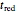 yields:
yields:  .
.
This agrees with the time for the blue bead and resolves the paradox.
A faster solution is to divide the two equations 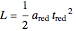 and
and 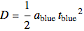 , which yields:
, which yields:
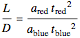 . Since
. Since  , the two times must be equal. Physically, the blue bead's acceleration is larger than the red bead's acceleration by the same ratio that the distance the blue bead travels is greater than the distance the red bead travels.
, the two times must be equal. Physically, the blue bead's acceleration is larger than the red bead's acceleration by the same ratio that the distance the blue bead travels is greater than the distance the red bead travels.
Source: T. B. Greenslade, Jr., "Galileo's Paradox," The Physics Teacher, 46(5), 2008 p. 294.
Permanent Citation