Gauss Code Loops

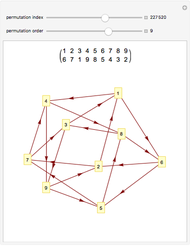
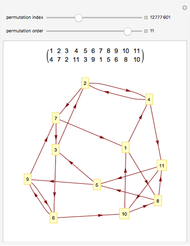
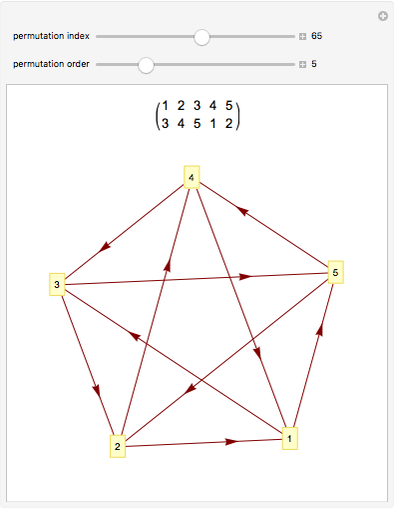
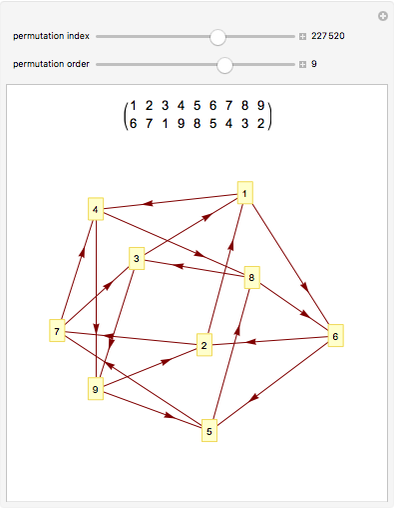
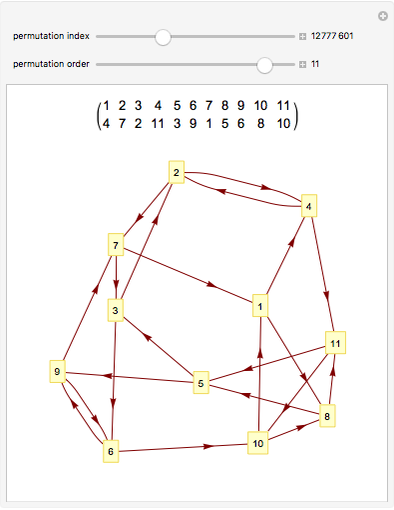
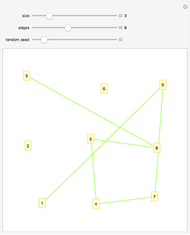
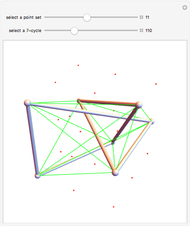
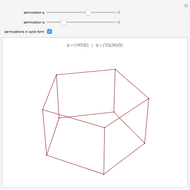
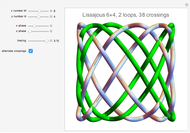
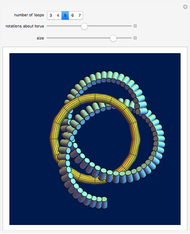
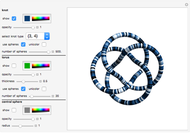
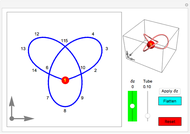
Draw a closed loop that crosses itself several times. Draw an arrow on the loop, then follow it, labeling every other intersection with 1, 2, 3, …, until the arrow is reached. Following these steps, every intersection will be labeled once, a fact noticed by Gauss. With additional steps, the Gauss code of the loop can be written, allowing reconstruction of the original diagram.

Considering every other intersection on the loop, one sequence is (1 2 3 …). The other sequence is a permutation. Thus, every self-intersecting closed loop corresponds to a permutation. The reverse is not true! For example, the permutation cannot be drawn as a loop with five intersections, because the underlying quartic graph is the nonplanar .

For orders 3, 4, 5, …, there are 3, 5, 16, 44, 180, … distinct graphs that come from the permutations. For orders 5, 6, and 7, there are 2, 36, and 571 permutations that cannot be drawn as self-intersecting loops due to nonplanarity. Some permutations may have parity issues that will prevent a Gauss code loop representation.