Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

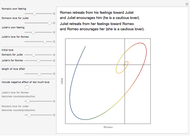
Gavrilov-Shilnikov Model

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

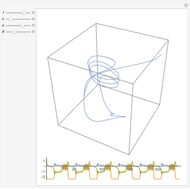
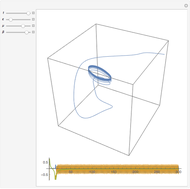
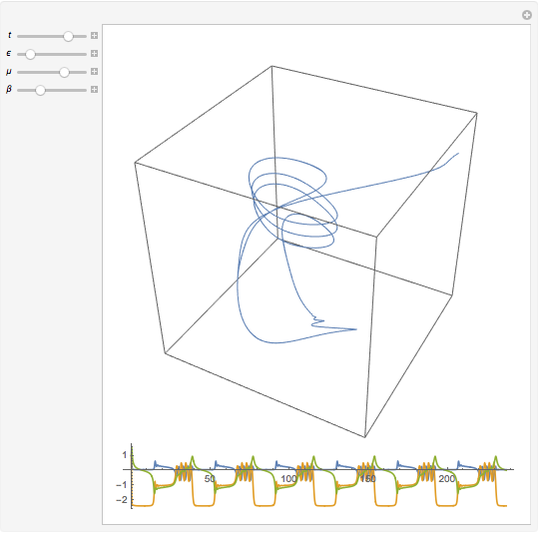
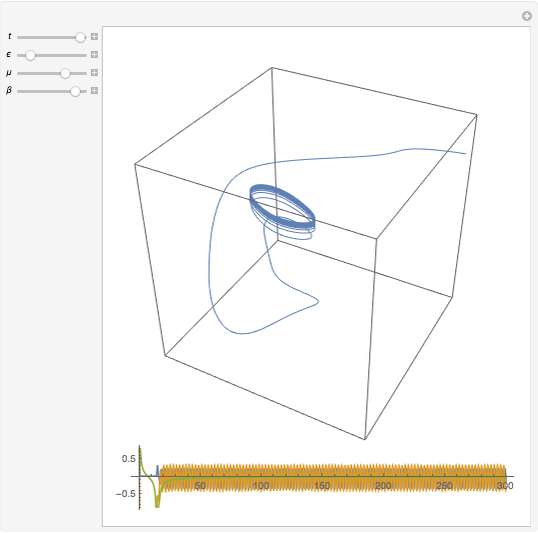
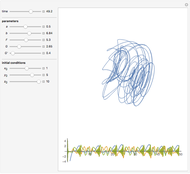
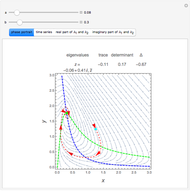
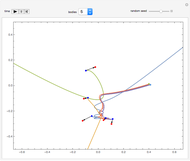
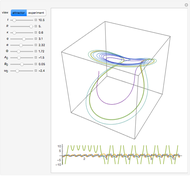
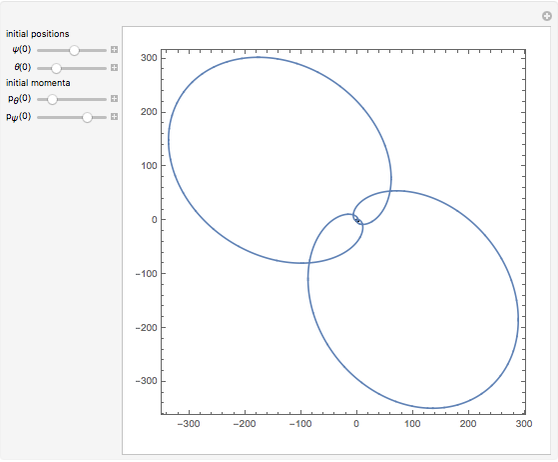
The Gavrilov–Shilnikov model exhibits a bifurcation known as the "blue-sky catastrophe", which is the last of the seven known bifurcations of a periodic orbit. This catastrophe creates a stable periodic orbit whose length and period increase without bound. Some applications include models for neuron activity and the operation of jet engines.

Contributed by: Enrique Zeleny (August 2012)
Open content licensed under CC BY-NC-SA

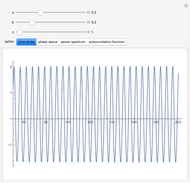
Snapshots

Details

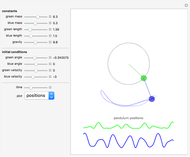
The relevant system of equations is

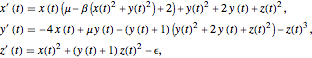
containing the empirical parameters , , and 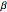. Plots of variables , , 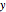and as functions of time appear at the bottom.

References

[1] A. Shilnikov and D. Turaev, "Blue-Sky Catastrophe," Scholarpedia, 2(8):1889, 2007. www.scholarpedia.org/article/Blue-sky_catastrophe.

[2] N. Gavrilov and A. Shilnikov, "Example of a Blue Sky Catastrophe," Methods of Qualitative Theory of Differential Equations and Related Topics, American Mathematical Society Translations, 2(200), (L. Lerman, G. Polotovskii, and L. Shilnikov, eds.), Providence, RI: American Mathematical Society, 2000 pp. 99–105.

[3] T. Vialar, Complex and Chaotic Nonlinear Dynamics, Berlin: Springer, 2009.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send