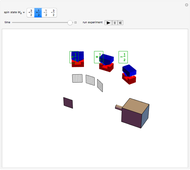
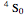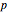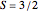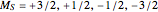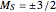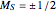Gedankenexperiment for Three Entangled Electrons: Analog of GHZ Photon Experiments

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
The classic experiments of Greenberger, Horne, and Zeilinger (GHZ) [1, 2, 3] show that entangled systems of three or four photons conform exactly to the laws of quantum mechanics, thus removing any lingering doubts about any deterministic local reality or hidden-value alternatives to quantum mechanics. These experiments confirm the statistical results implying violations of Bell's inequalities, with the advantage that definite outcomes are obtained, rather than statistical distributions.
[more]
Contributed by: S. M. Blinder (May 2013)
Open content licensed under CC BY-NC-SA
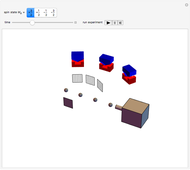
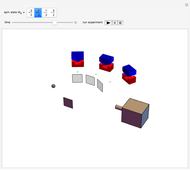
Snapshots
Details
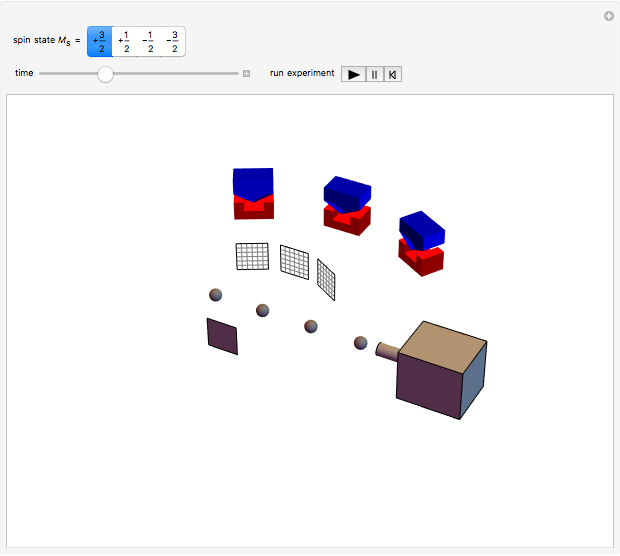
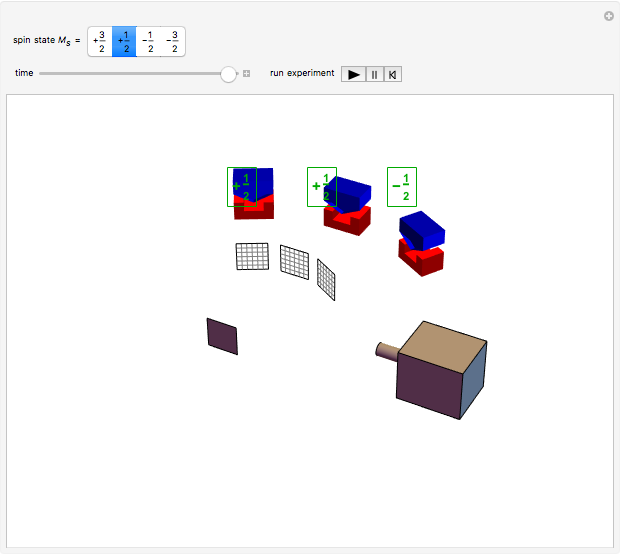
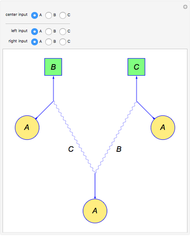
Three parallel entangled electron spins not constrained by the Pauli principle can be represented by one of four possible spin wavefunctions: 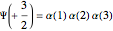 ,
,  , with the obvious analogs for
, with the obvious analogs for 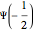 and
and 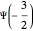 . In each of the
. In each of the 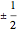 states, two spins are entangled with parallel spins, while the third spin is antiparallel. This can happen in three different ways, which also reflects the indeterminacy of quantum mechanics.
states, two spins are entangled with parallel spins, while the third spin is antiparallel. This can happen in three different ways, which also reflects the indeterminacy of quantum mechanics.
References
[1] D. Greenberger, M. Horne, A. Shimony, and A. Zeilinger, "Bell's Theorem without Inequalities," American Journal of Physics, 58(12), 1990 pp. 1131–1143. doi:10.1119/1.16243.
[2] D. Mermin, "Quantum Mysteries Revisited," American Journal of Physics, 58(8), 1990 pp. 731–734. doi:10.1119/1.16503.
[3] S. M. Blinder, Introduction to Quantum Mechanics, Amsterdam: Elsevier, 2004 pp. 277–280.
Permanent Citation