Generalized Coons Surface

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
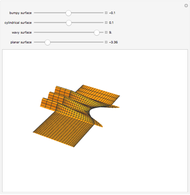
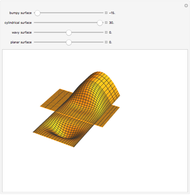
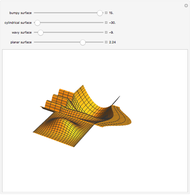
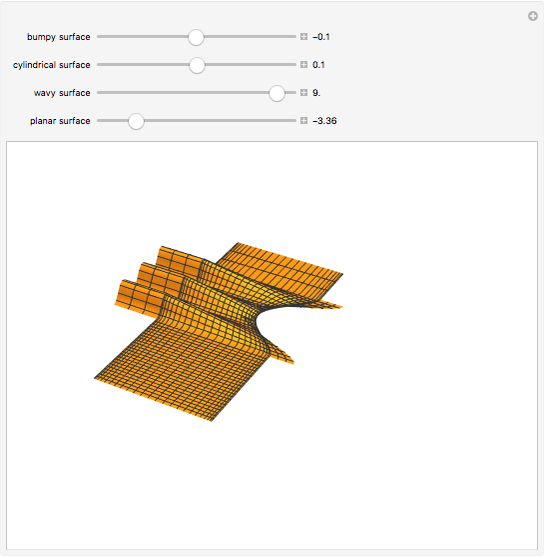
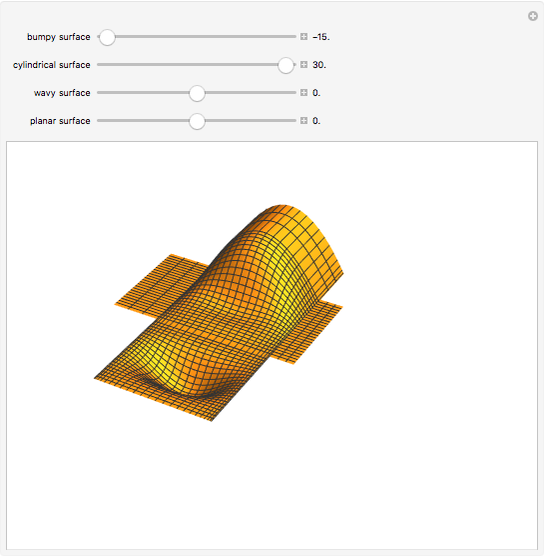
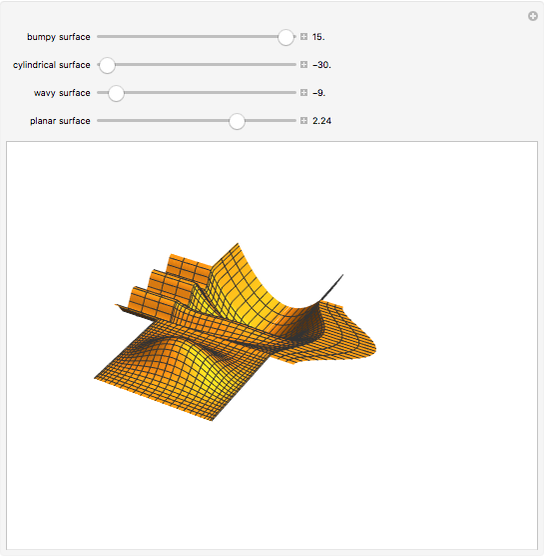
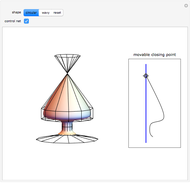
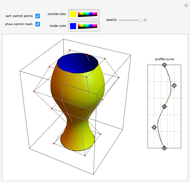
The generalized Coons surface (shown in the middle) is defined by four rectangular surface patches. By changing the shape of the constituents, the shape of the resulting surface will change as well, even if the boundary lines are fixed. This case can be illustrated by changing the bump on the patch in the front.
Contributed by: M. Szilvasi-Nagy (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The classical Coons surface is generated by its four boundary curves. Instead of four curves, four surface patches are the input data of this generalized Coons surface. The four patches are defined on the same parameter domain, and one boundary curve of each forms a side of a curvilinear rectangle. The resulting surface interpolates these boundary curves, and its shape is influenced also by the shapes of the constituent parts. This surface can be applied for filling holes in a composite surface, where not only the hole but also the surrounding surfaces are considered. The construction presented ensures only a 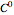 continuous connection of the generated surface to the constituent parts along their common boundary curves.
continuous connection of the generated surface to the constituent parts along their common boundary curves.
References:
M. Szilvasi-Nagy, P. T. Vendel, and H. Stachel,  Filling of Gaps by Convex Combination of Surfaces under Boundary Constraints," KoG, Information Journal of Croatian Society of Constructive Geometry and Computer Graphics, 6, 2002 pp. 41–48.
Filling of Gaps by Convex Combination of Surfaces under Boundary Constraints," KoG, Information Journal of Croatian Society of Constructive Geometry and Computer Graphics, 6, 2002 pp. 41–48.
M. Szilvasi-Nagy and I. Szabó, "Generalization of Coons' Construction," Computers & Graphics, 30, 2006 pp. 588–597.
Permanent Citation