Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Generalized Ulam Sets in the Plane

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

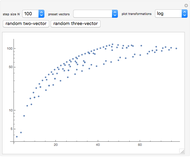
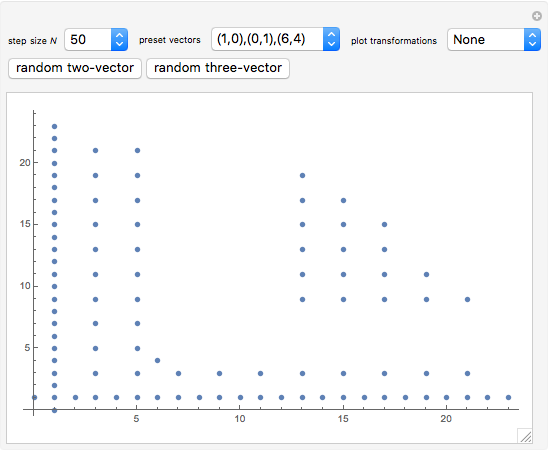
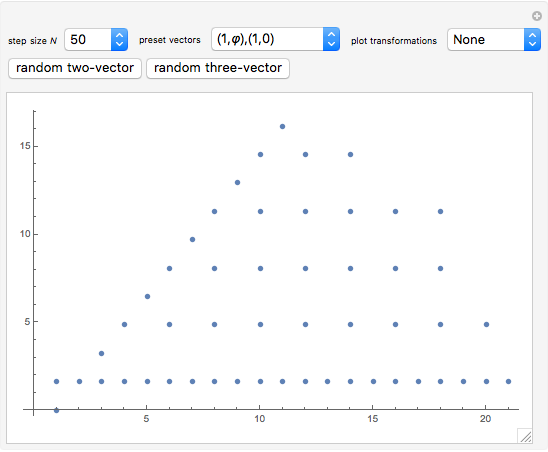
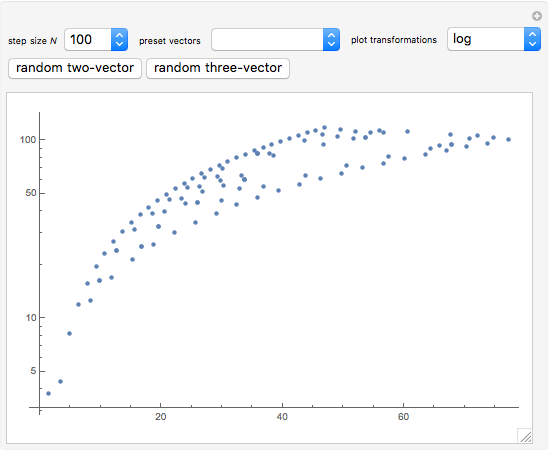
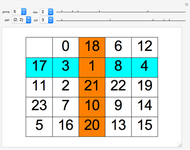
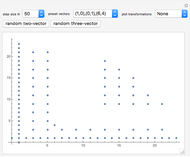
This Demonstration plots a list of points of the generalized Ulam set 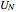in the plane after 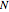steps of iteration. The recursive rule to generate 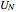is to append vectors to the previous set of minimal Euclidean norms that can be uniquely written as the sum of two distinct vectors from 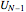. The specified list of linearly independent initial vectors completely determines the points.

[more]

Set the "step size " for the plot, keeping in mind that any setting may be slow.

The list of two or more initial vectors may be specified by selecting one of the preset initial vector combinations or randomly.

[less]

Contributed by: Maxie D. Schmidt (August 2017)
Suggested by: Jayadev Athreya and his work with the WXML at the University of Washington
Open content licensed under CC BY-NC-SA

Snapshots

Details

References

[1] N. Kravitz and S. Steinerberger, "Ulam Sequences and Ulam Sets." arxiv.org/abs/1705.01883.

[2] M. D. Schmidt, "Pair Correlation and Gap Distributions for Substitution Tilings and Generalized Ulam Sets in the Plane." arxiv.org/abs/1707.05509.

[3] M. D. Schmidt. "Ulam-sets." (Jul 31, 2017) github.com/maxieds/Ulam-sets.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send