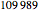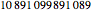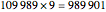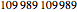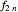Generating 9-Flips

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
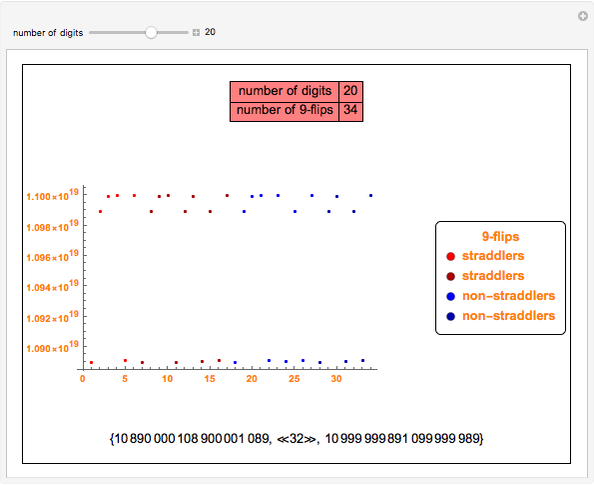
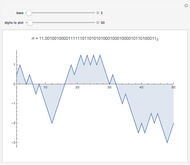
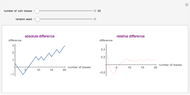
A 9-flip is a number that when multiplied by 9 has its digits reversed (e.g. 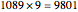 ). This Demonstration shows and counts all 9-flips for numbers with 1 to 30 digits.
). This Demonstration shows and counts all 9-flips for numbers with 1 to 30 digits.
Contributed by: Roberta Grech (February 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
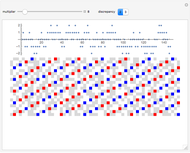
The code used to generate the 9-flips was built on the solution suggested in Exercise 55 of [1], p. 115.
A straddler with 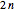 digits can be obtained from a non-straddler with
digits can be obtained from a non-straddler with 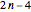 digits by inserting 1089 as a central block (shown in red) or by inserting 99 in the center of a straddler with
digits by inserting 1089 as a central block (shown in red) or by inserting 99 in the center of a straddler with 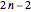 digits (shown darker red).
digits (shown darker red).
A non-straddler with 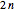 digits can be obtained from a non-straddler with
digits can be obtained from a non-straddler with 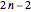 digits by inserting 00 as a central block (shown in blue) or by inserting 8910 in the center of a straddler with
digits by inserting 00 as a central block (shown in blue) or by inserting 8910 in the center of a straddler with 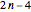 digits (shown darker blue).
digits (shown darker blue).
A 9-flip with an odd number of digits (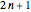 ) can be obtained from a straddler with
) can be obtained from a straddler with 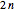 digits by inserting a 9 in the center (shown red or darker red) or from a non-straddler with
digits by inserting a 9 in the center (shown red or darker red) or from a non-straddler with 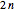 digits by inserting a 0 in the center (shown blue or darker blue).
digits by inserting a 0 in the center (shown blue or darker blue).
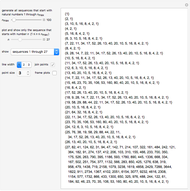
Hence the number of 9-flips with an odd number of digits (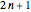 ) is equal to the number of 9-flips with an even number of digits (
) is equal to the number of 9-flips with an even number of digits (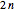 ), and this sequence of numbers of 9-flips with an odd number of digits (
), and this sequence of numbers of 9-flips with an odd number of digits (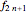 ) is also a Fibonacci sequence obeying the recurrence relation
) is also a Fibonacci sequence obeying the recurrence relation 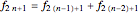 .
.
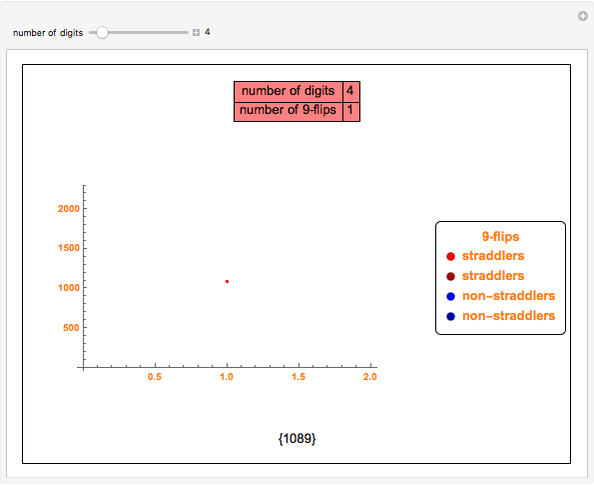
Snapshot 1: the first nonzero 9-flip is 1089 (a straddler), with four digits.
Snapshot 2: with five digits, the only 9-flip is 10989 (a straddler), obtained by inserting a 9 in the center of the four-digit flip.
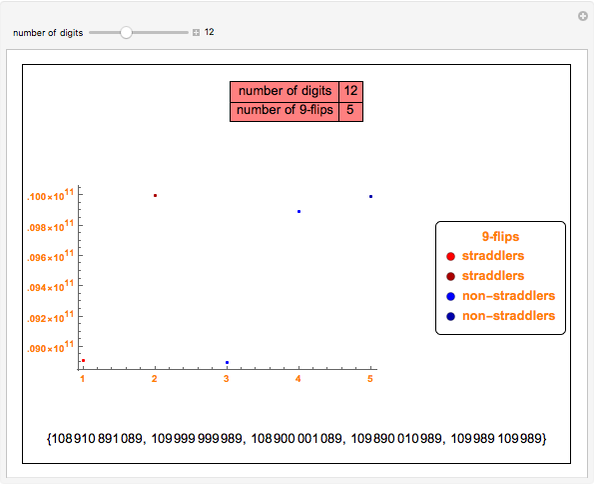
Snapshot 3: with eight digits, there are two 9-flips, a straddler (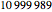 ) and a non-straddler (
) and a non-straddler (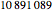 ) that can be split into two halves.
) that can be split into two halves.
Snapshot 4: with 30 digits, there are 377 9-flips, consisting of a mixture of straddlers and non-straddlers.
Reference
[1] A. Gardiner, Discovering Mathematics: The Art of Investigation, Mineola, NY: Dover Publications, 2006 pp. 63–118.
Permanent Citation