Generating a Cardioid VII: Joining Points on a Circle

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
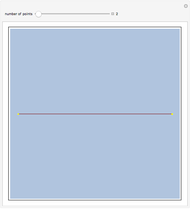
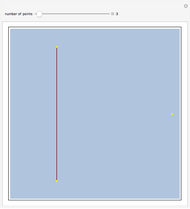
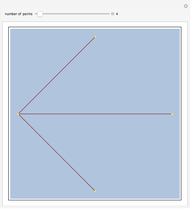
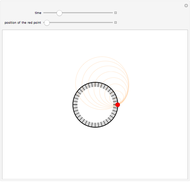
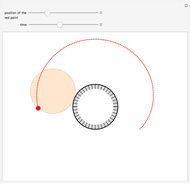
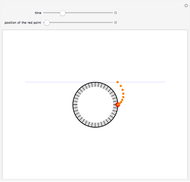
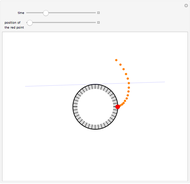
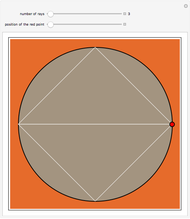
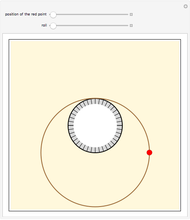
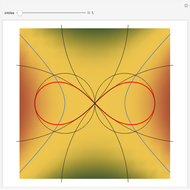
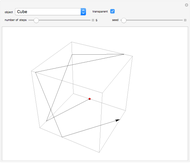
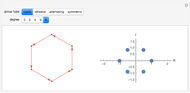
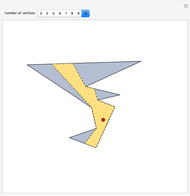
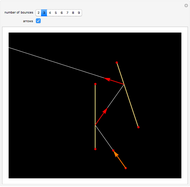
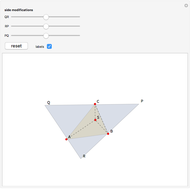
Consider  points equally spaced on a circle. Connect the
points equally spaced on a circle. Connect the 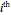 point to the
point to the 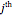 point, where
point, where 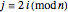 . As
. As 
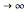 , the lines tend to the envelope of a cardioid.
, the lines tend to the envelope of a cardioid.
Contributed by: Jaime Rangel-Mondragon (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Generating a Cardioid VII: Joining Points on a Circle"
http://demonstrations.wolfram.com/GeneratingACardioidVIIJoiningPointsOnACircle/
Wolfram Demonstrations Project
Published: March 7 2011