Generating Lissajous Figures

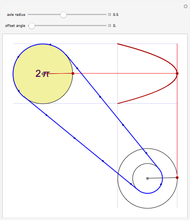
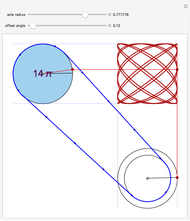
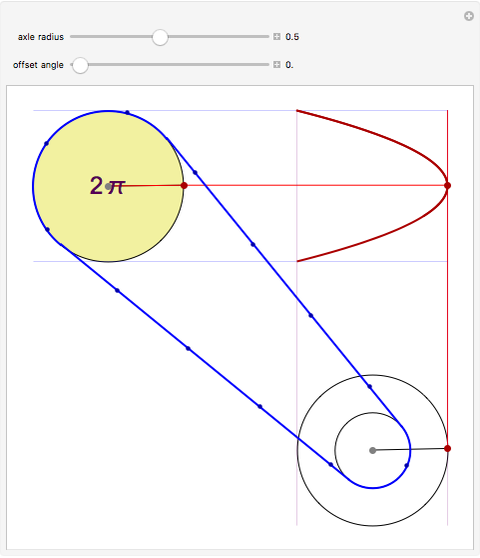
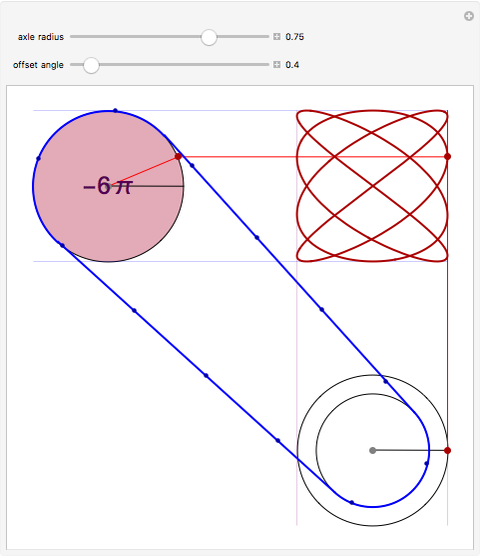
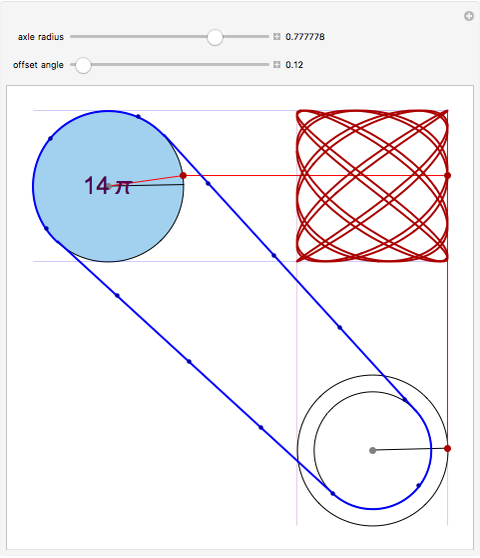
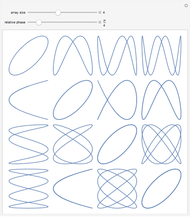
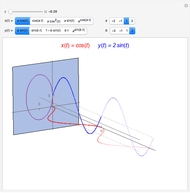
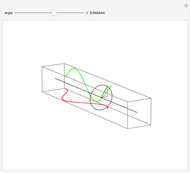
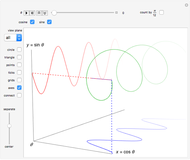
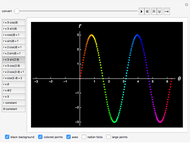
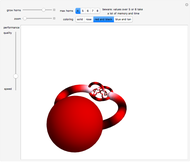
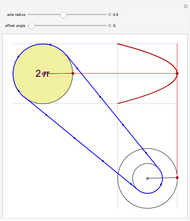
Given two wheels connected by a belt and a point on the outer rim of each, one can generate a Lissajous figure by the motion of the wheels. The coordinates of a point on a wheel can be described by sine functions of a certain frequency and phase shift. The ratio of the radii at the ends of the belt determines the relative frequencies of the 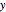coordinate of the red point on the upper left wheel and the coordinate of the red point on the lower right wheel. If the starting position of a point on a wheel is offset by a certain angle, a phase shift occurs in the sine functions describing the coordinates of the point.

Drag either red point to move both wheels and the curve will be traced. You can change the radius of the axle on the lower right wheel and the offset angle between the starting positions of the points with the sliders. The radius controls the relative frequency of the and coordinates. When it is a rational number, a closed curve is generated; when it is irrational, the curve never closes and fills the square. The offset angle determines the phase shift of the coordinate of the red point of the upper left wheel and affects the shape of the Lissajous figure generated.