Geodesic Balls in the Nil-Space
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
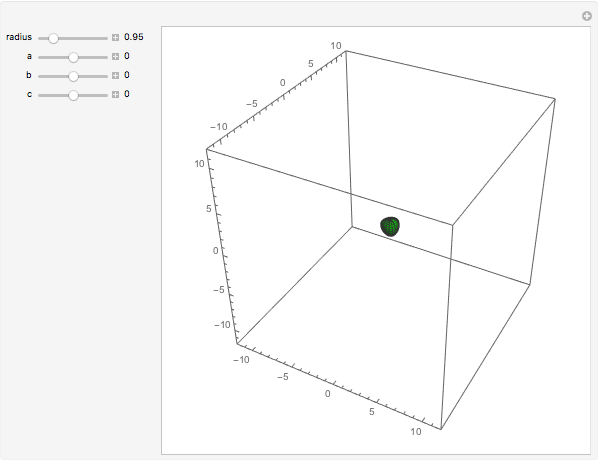
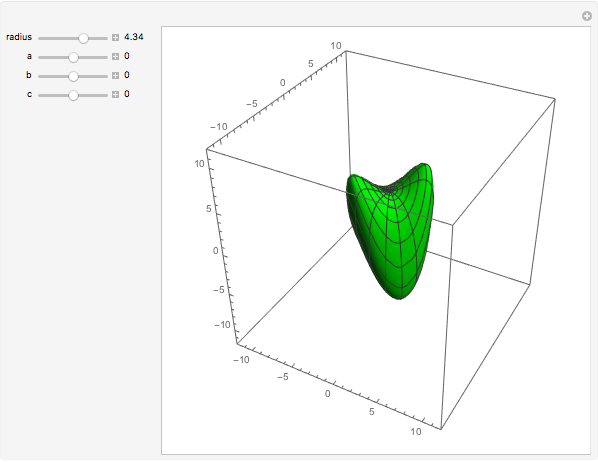
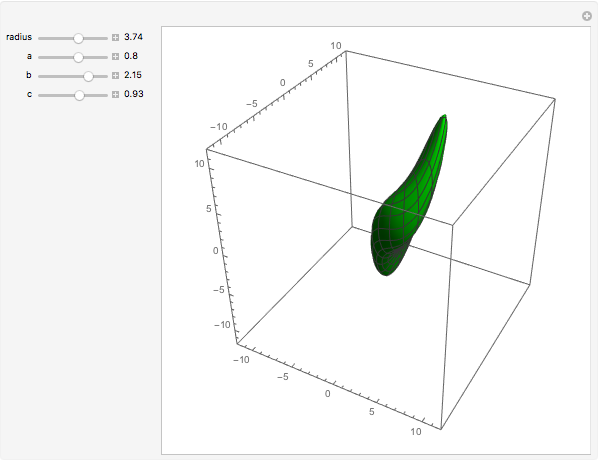
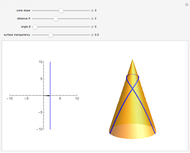
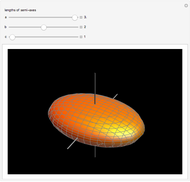
W. Heisenberg's real matrix group provides a noncommutative translation group of an affine 3-space. The Nil-geometry, which is one of the eight Thurston 3-geometries, can be derived from this group. It was proved by E. Molnár that the homogeneous 3-spaces have a unified interpretation in the projective 3-sphere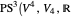 
). In this Demonstration we visualize the geodesic balls of the Nil-space with the origin as the center, radius in 
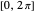, and translated by 
.
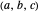Contributed by: Benedek Schultz, János Pallagi (April 2009)
Suggested by: Jenő Szirmai
Open content licensed under CC BY-NC-SA
Snapshots
Details
We get the geodesic ball by rotating the following curve about the 
axis (lying in the plane 
): 
, 
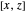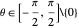if 
; if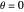 
: 
, 
.
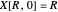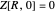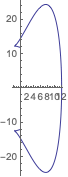
If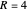 
, then the curve is basically half of the intersection of the geodesic sphere with the [
, 
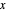] plane and looks like this:
The coordinates of a point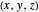 
rotated by 
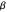around the 
axis are (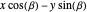
, 
, 
).
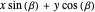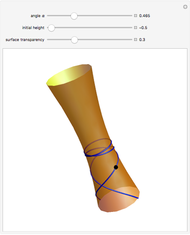
Finally, we can translate the geodesic sphere with a vector (
, 
, 
) to get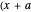 
, 
, 
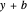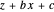). This translation is defined by left multiplication with Heisenberg's matrix:
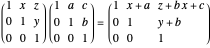
It is a good idea to zoom in for a better view as well as to rotate the image.
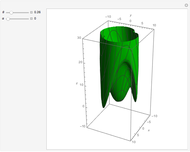
If the radius is less than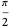 
, then the ball is convex in the affine-Euclidean sense of our model, but if the radius is in 
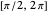, then it is not convex. Also the geodesic sphere exists in Nil if and only if 
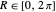. For example if 
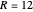, then the curve used to rotate about the 
axis would be:
Reference:
J. Szirmai, "The Densest Geodesic Ball Packing by a Type of Nil Lattices," Beiträge zur Algebra und Geometrie (Contributions to Algebra and Geometry), 48(2), 2007 pp. 383-397.
Permanent Citation
Geodesic Cone in Nil-Geometry
Benedek Schultz and János Pallagi
Torus in Nil-Space
Benedek Schultz and János Pallagi
Cone Geodesics
Antonin Slavik
Hyperboloid Geodesics
Antonin Slavik
Geodesics and Conjugate Loci on a Torus
Matthew Cherrie and Thomas Waters
Catalan's Surface
Enrique Zeleny
Views of the Costa Minimal Surface
Enrique Zeleny
Ellipsoid
Jeff Bryant
Surfaces of Revolution with Constant Gaussian Curvature
Antonin Slavik
Dupin's Indicatrix of a Torus
Sonja Gorjanc and Desana ?tambuk
