Geometry of Two-Variable Laguerre Polynomials

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
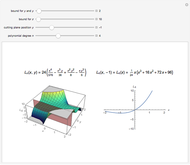
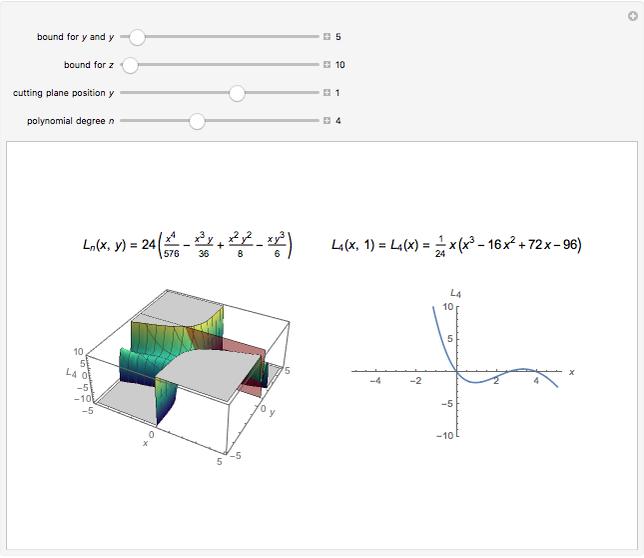
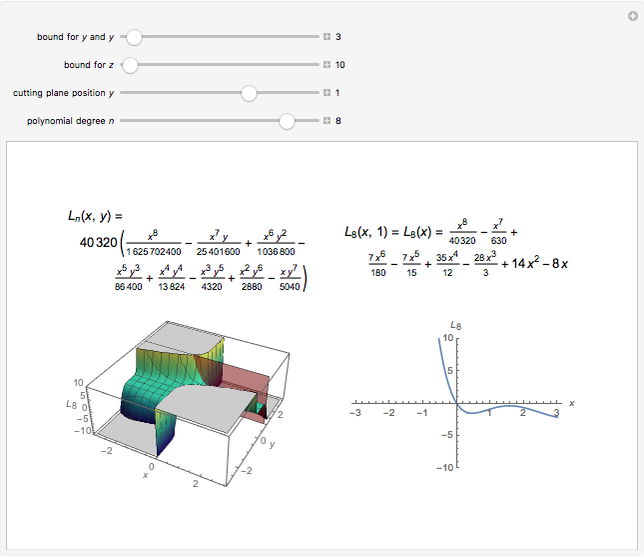
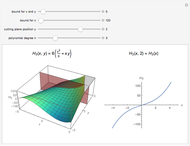
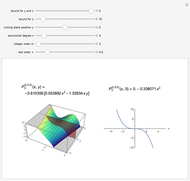
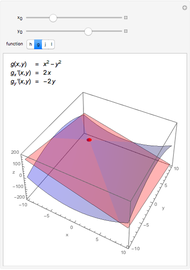
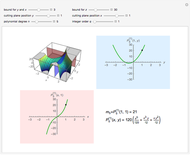
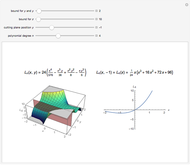
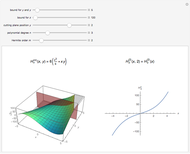
On the left is a three-dimensional plot of a Laguerre polynomial in two variables  and
and  ; on the right is a two-dimensional plot of the surface cut by a plane perpendicular to the
; on the right is a two-dimensional plot of the surface cut by a plane perpendicular to the  axis. The exponential operator transform is defined in the Details.
axis. The exponential operator transform is defined in the Details.
Contributed by: Marcello Artioli and Giuseppe Dattoli (June 2015)
Open content licensed under CC BY-NC-SA
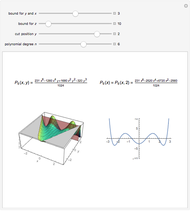
Snapshots
Details
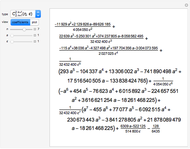
The two-variable Laguerre polynomials

have been shown to be solutions of the following partial differential equation:
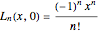 .
.
The operator

is called the Laguerre derivative since
 ,
,
and it exhibits the following notable property:
 .
.
Therefore, it is easily shown that the solution of the above equations, written in an operational form, reads:
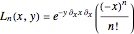 .
.
The preceding formulas suggest geometrical representations for the two-variable Laguerre polynomials, which are displayed in the graphics. The exponential operator transforms an ordinary monomial  into a polynomial of the Laguerre type. The monomial-to-polynomial transition is shown by moving the cutting plane orthogonal to the
into a polynomial of the Laguerre type. The monomial-to-polynomial transition is shown by moving the cutting plane orthogonal to the  axis. For a specific value of the polynomial degree
axis. For a specific value of the polynomial degree  , the polynomials
, the polynomials  lie on the cutting plane.
lie on the cutting plane.
References
[1] P. Appell and J. K. de Fériet, Fonctions hypergéométriques et hypersphériques: polynômes d'Hermite, Paris: Gauthier-Villars, 1926.
[2] G. Dattoli, "Generalized Polynomials, Operational Identities and Their Applications," Journal of Computational and Applied Mathematics, 118(1–2), 2000 pp. 111–123. doi:10.1016/S0377-0427(00)00283-1.
Permanent Citation