Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

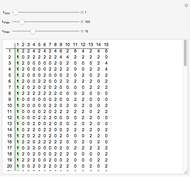
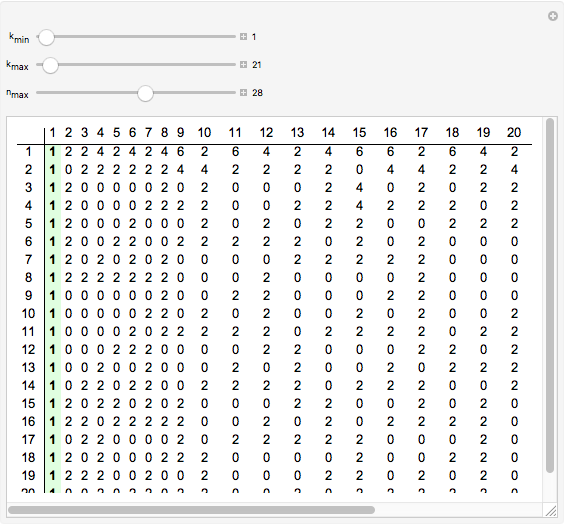
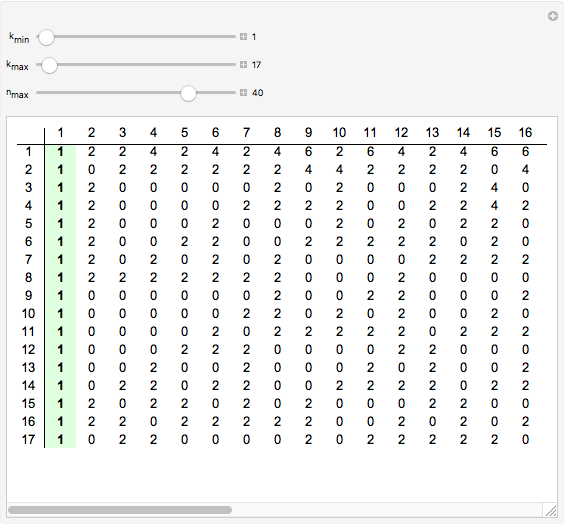
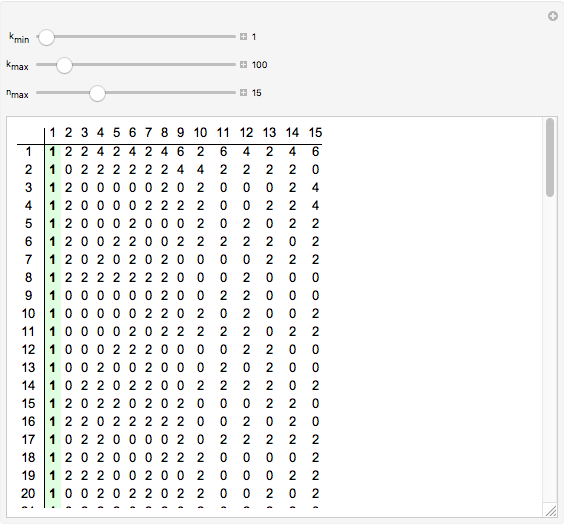
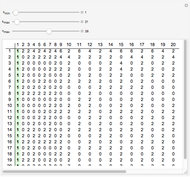
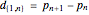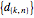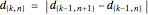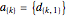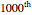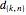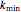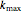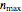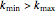Gilbreath's Conjecture

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

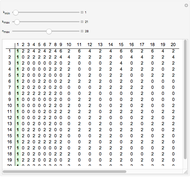
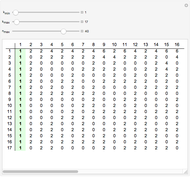
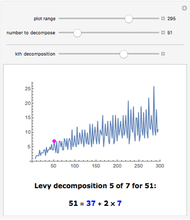
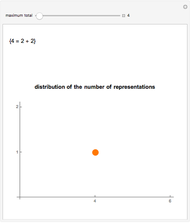
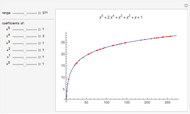
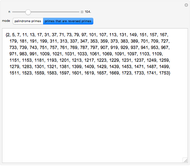
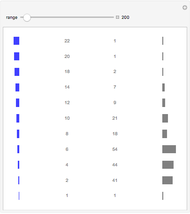
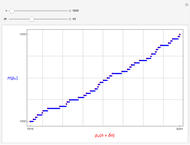
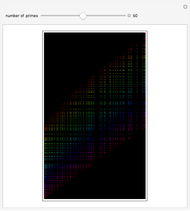
A surprising conjecture about the gaps between primes, namely: Let 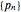denote the ordered sequence of prime numbers 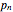, and define each term in the sequence 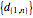by

[more]

,

where is positive. Also, for each integer greater than 1, let the terms in be given by

.

Gilbreath's conjecture states that every term in the sequence is 1. With this Demonstration you can check this amazing statement up to the difference series. The controls let you see the matrix of , where goes from to , and goes from 1 to . (If , they switch roles. )

[less]

Contributed by: Peter Bohus and Márton Károlyi (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send