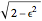Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Glissettes and the Orthoptic Curve of the Ellipse

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

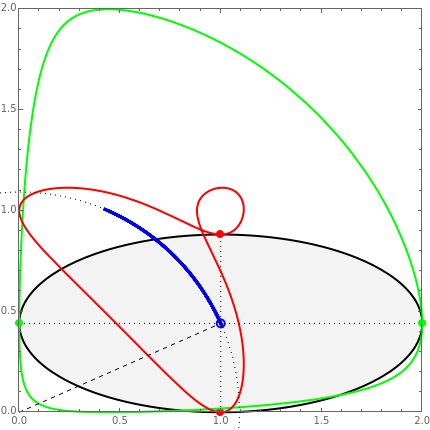
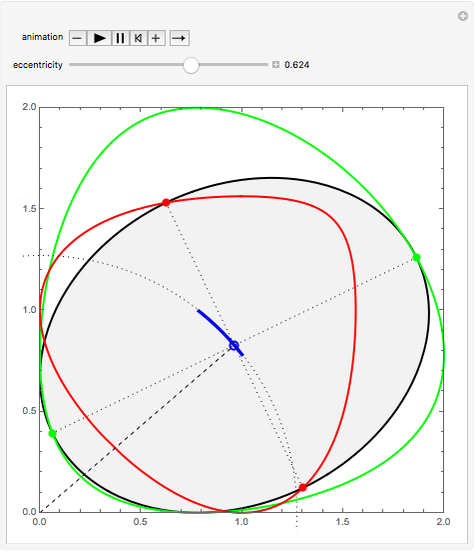
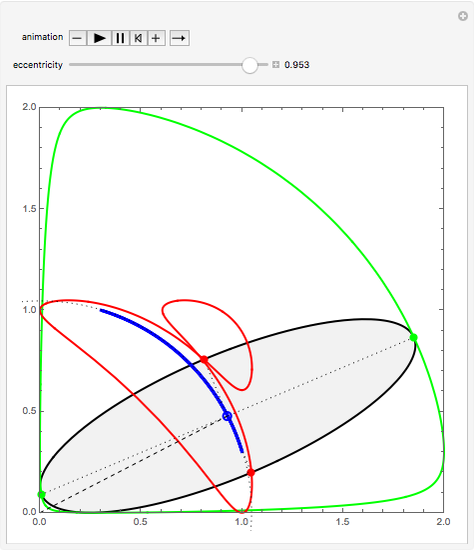
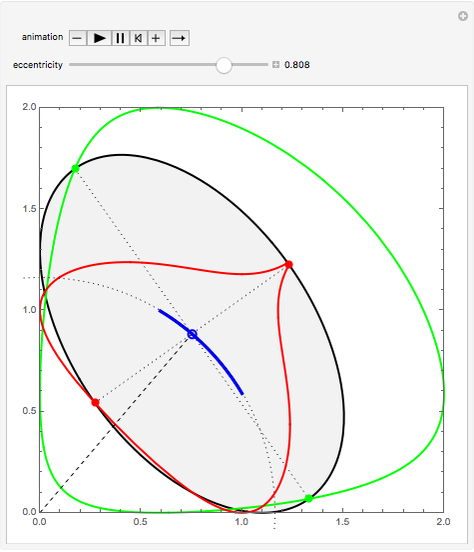
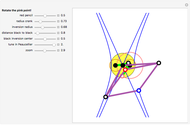
A glissette is the geometrical locus of a point fixed to a curve sliding inside another curve. This Demonstration shows three different glissettes that are formed by points of an ellipse sliding inside a pair of orthogonal lines (the and axes).

[more]

The blue glissette curve is traced by the center of the ellipse.

The green and red glissettes are traced by the extreme points on the semimajor and semiminor axes.

The glissette formed by the center of the ellipse is a sector of a circle with radius because the orthoptic curve of an ellipse is a circle. The orthoptic curve of an ellipse is the locus of the points from which the ellipse can be viewed under a right angle, in this case the two orthogonal axes.

[less]

Contributed by: Erik Mahieu (February 2012)
Open content licensed under CC BY-NC-SA

Snapshots

Details

An interesting collection of glissettes can be found in [1].

Reference

[1] R. Ferréol. "Encyclopédie des Formes Mathématiques Remarquables." Mathcurve. www.mathcurve.com.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send