Global B-Spline Curve Fitting by Least Squares

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
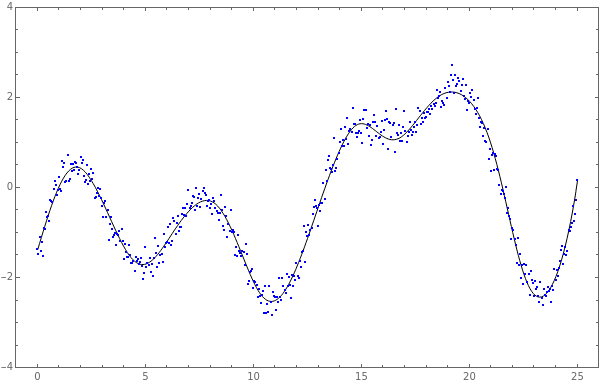
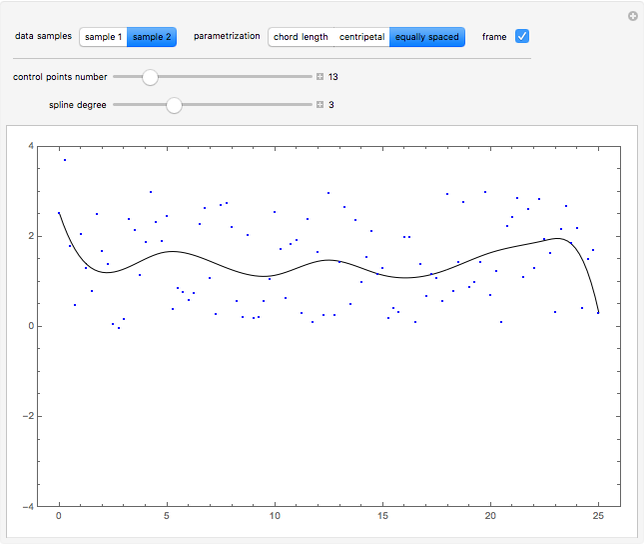
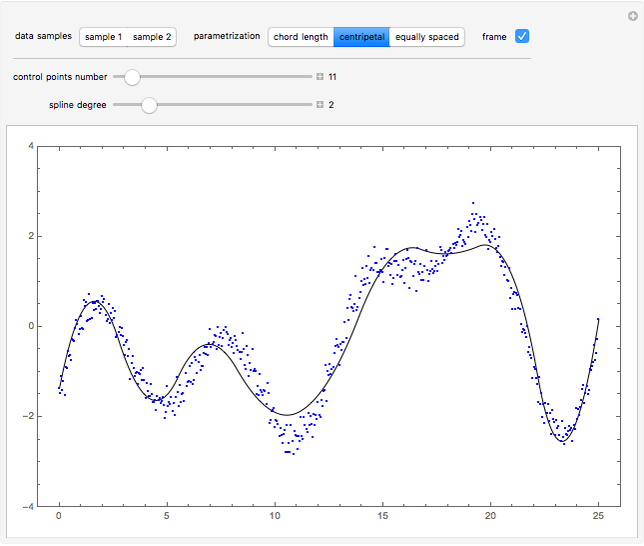
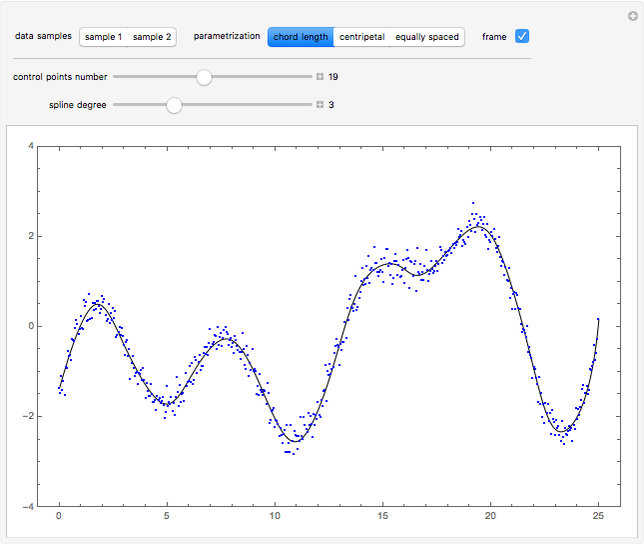
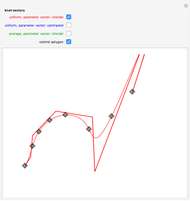
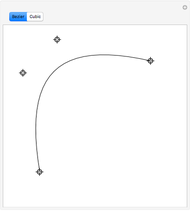
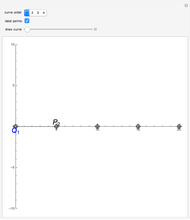
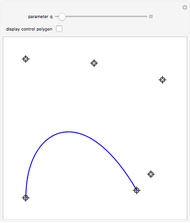
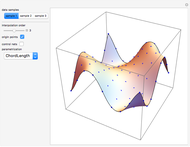
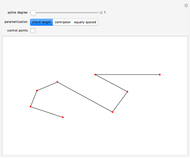
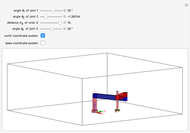
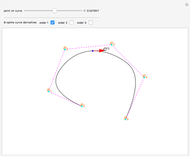
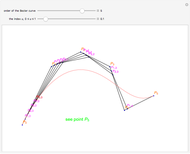
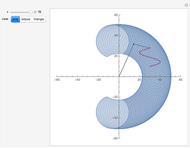
This Demonstration shows global B-spline curve fitting by the least-squares method. B-splines are a generalization of Bezier curves. In a B-spline, each control point is associated with a particular basis function. The implementation is fully described in the Details.
Contributed by: Shutao Tang (October 2015)
(Northwestern Polytechnical University, Xi'an City, China)
Open content licensed under CC BY-NC-SA
Snapshots
Details
For definitions and details of the B-spline curve and B-spline basis function, see Related Links.
Assume that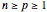 and
and  are given, where
are given, where 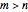 . We seek a
. We seek a 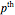 -degree nonrational curve
-degree nonrational curve
 ,
, 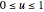 ,
,
satisfying
(1) 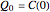 ,
, 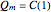 ,
,
(2) the remaining  are approximated in the least-squares sense; that is,
are approximated in the least-squares sense; that is,
 is a minimum with respect to the
is a minimum with respect to the  variables.
variables.
Here, 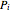 and
and 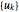 are precomputed parameter values.
are precomputed parameter values.
Let
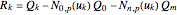 ,
, 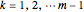 .
.
Then set
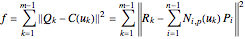
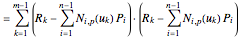
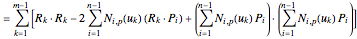 .
.
So 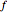 is a scalar-valued function of the
is a scalar-valued function of the  variables
variables  . Applying the standard technique of linear least-squares fitting to minimize
. Applying the standard technique of linear least-squares fitting to minimize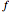 , set the derivatives with respect to the
, set the derivatives with respect to the  points,
points, 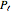 , to zero. The
, to zero. The 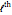 of these derivatives is
of these derivatives is
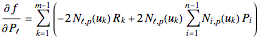 ,
,
which implies that
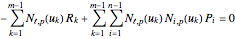 .
.
It follows that
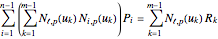 . (1)
. (1)
Equation (1) is one linear equation in the unknowns 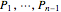 . Letting
. Letting  yields the system of
yields the system of  equations in
equations in  unknowns,
unknowns,
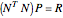 ,
,
where 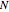 is the
is the 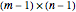 matrix of scalars
matrix of scalars
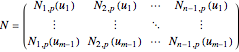 , (2)
, (2)
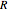 is the vector of
is the vector of  points
points
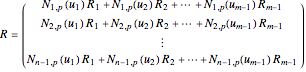 , (3)
, (3)
and
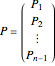 .
.
In order to set up equations (2) and (3), a knot vector 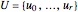 with parameters
with parameters 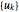 is required.
is required.
The 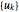 can be computed using the following method (with
can be computed using the following method (with 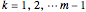 , in each case):
, in each case):
(1) Equally spaced
 ,
, 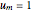 ,
, 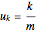
(2) Chord length
let  , then
, then
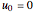 ,
, 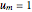 ,
, 
(3) Centripetal
let 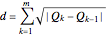 , then
, then
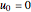 ,
, 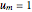 ,
, 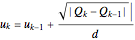
The placement of the knots should reflect the distribution of the 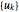 . If
. If 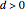 , denote by
, denote by 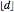 the largest integer less than or equal to
the largest integer less than or equal to  . We need a total of
. We need a total of 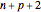 knots; there are
knots; there are  internal knots and
internal knots and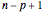 internal knot spans.
internal knot spans.
Let
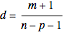 .
.
Then define the internal knots by
 ,
, 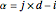 ,
,
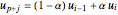 ,
, 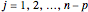 . (4)
. (4)
Equation (4) guarantees that every knot span contains at least one 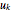 , and under this condition the matrix
, and under this condition the matrix  is positive definite and well-conditioned.
is positive definite and well-conditioned.
Reference
[1] L. Piegl and W. Tiller, The NURBS Book, 2nd ed., Berlin: Springer-Verlag, 1997 pp. 410–413.
Permanent Citation