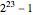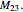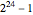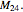Golay Code

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
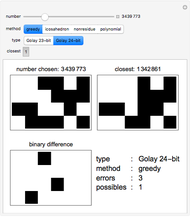
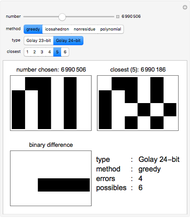
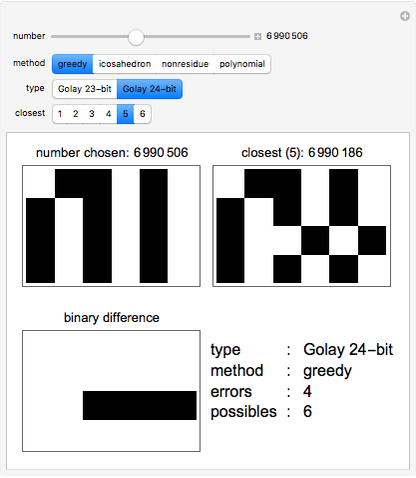
When Voyager visited Saturn and Jupiter, data for the pictures used blocks of Golay code. Each 24-bit block of data could have up to three errors, and the computers here on Earth could fix these errors. The Golay code is thus an error-correcting code. It was originally published in 1949 with Marcel Golay's half-page paper, "Notes on Digital Coding". Today, this paper is considered one of the most remarkable papers ever published, with deep, deep connections to group theory, graph theory, number theory, combinatorics, game theory, multidimensional geometry, and even particle physics.
[more]
Contributed by: Ed Pegg Jr (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
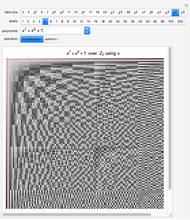
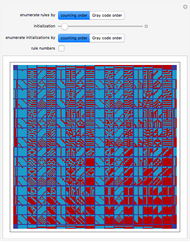
This Demonstration builds the Golay code in four different ways.
1. Greedy method. Start a list with the 24-bit 0 word (000…000). Add the first 24-bit word that has eight or more differences from all words in the list. Repeat, to get the 4096 code words. The code words are winning positions in the game of Mogul, played with 24 coins in a row. Each turn flips between one and seven coins such that the leftmost flipped coin goes from heads to tails. Last to move wins.
2. Icosahedron method. Start with the adjacency matrix of an icosahedron, and append the 12×12 matrix 1-I. These 12 vectors serve as a basis for the 4096 code words.
3. Nonresidue method. If an integer is squared modulus 23, the result will not be in 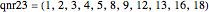 , the quadratic nonresidues mod 23. In a 24-bit code word, change those places to 1. Obtain 11 more lists by adding 1 to 11 to
, the quadratic nonresidues mod 23. In a 24-bit code word, change those places to 1. Obtain 11 more lists by adding 1 to 11 to  , mod 23. Finally, change the
, mod 23. Finally, change the 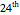 bit of each to 1 and gain a basis for the 4096 code words.
bit of each to 1 and gain a basis for the 4096 code words.
4. Polynomial method. Modulus 2, one factor of 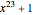 is
is  Consider the powers of
Consider the powers of 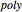 , namely
, namely 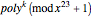 . There are 253 polynomials with seven terms. Choose 12 polynomial powers with differing initial terms, and append 1 to each polynomial's coefficient list to obtain a basis for the 4096 code words.
. There are 253 polynomials with seven terms. Choose 12 polynomial powers with differing initial terms, and append 1 to each polynomial's coefficient list to obtain a basis for the 4096 code words.
M. J. E. Golay, "Notes on Digital Coding," Proc. IRE, 37, 1949 p. 657.
J. H. Conway and N. J. A. Sloane, Sphere Packings, Lattices, and Groups, 3rd ed., New York: Springer, 1999.
Permanent Citation