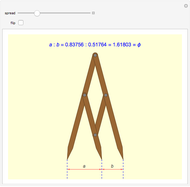
Golden Ratio Dividers

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
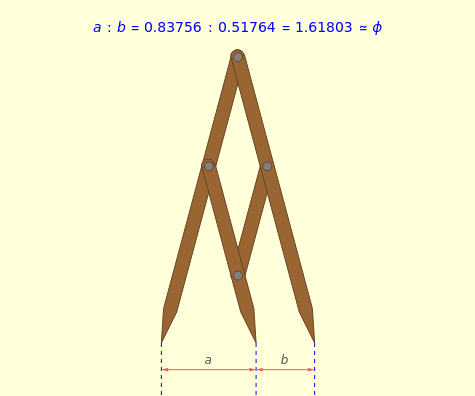
This tool can be used to determine whether two measurements occur in the golden ratio (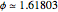 ). Regardless of the angle between the outermost arms of the divider, the golden ratio is seen between the intervals created by the outer and middle arms, and between the total span of the dividers and the larger interval.
). Regardless of the angle between the outermost arms of the divider, the golden ratio is seen between the intervals created by the outer and middle arms, and between the total span of the dividers and the larger interval.
Contributed by: Steve Strain (Slippery Rock University of Pennsylvania) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The divider modeled here finds use in a diverse range of fields—art, graphic design, dental cosmetics, and many others—for laying out measurements that are in the golden ratio proportion. One way of defining the golden ratio is to divide an interval into two subintervals such that the ratio of the whole interval to the larger subinterval is equal to the ratio of the larger subinterval to the smaller. Or, using the variable names from this model with  the larger subinterval:
the larger subinterval: 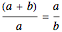 . Regardless of how far the divider is opened, the same relationship can be seen among the whole interval and subintervals between the arms.
. Regardless of how far the divider is opened, the same relationship can be seen among the whole interval and subintervals between the arms.
It is possible to design similar dividers in which the arms create intervals in proportions other than the golden ratio, but for none of these does the same equality of proportions hold true. Additionally, the physical construction of a golden ratio divider shows an elegance not shared by dividers measuring other proportions: regardless of the total length of an arm, the pivot points on each of the three arms divide them into segments that are in the same proportion—not surprisingly, the golden ratio.
Snapshot 1: opened to 15°, the divider creates intervals  and
and  related by the golden ratio,
related by the golden ratio, 
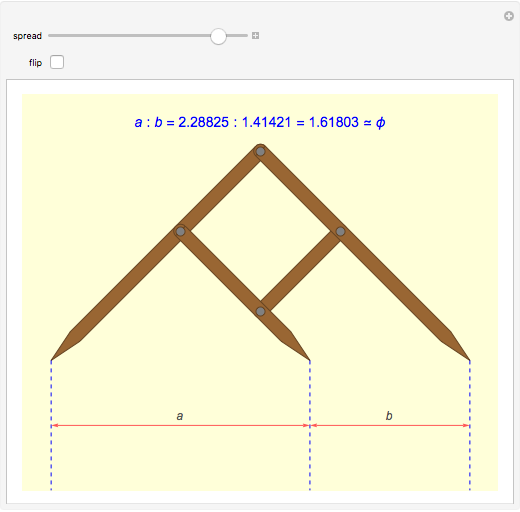
Snapshot 2: opened to 90°, the same relationship between  and
and  is true
is true
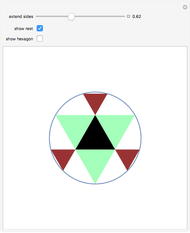
Snapshot 3: opened to 15°, but with  now the smaller interval, the divider demonstrates a relation unique among positive numbers to the golden ratio:
now the smaller interval, the divider demonstrates a relation unique among positive numbers to the golden ratio: 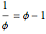
Permanent Citation