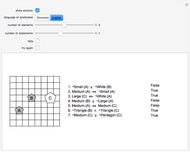
Goodstein Function in Terms of Fast-Growing Function Hierarchies

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
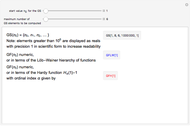
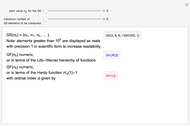
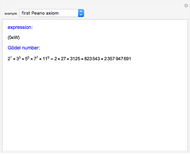
Goodstein's theorem (GT) is a natural independence phenomenon. GT is the combinatorial statement that for each integer  , the associated Goodstein sequence (GS) eventually reaches zero. This statement is true but unprovable in Peano arithmetic (PA). For each integer
, the associated Goodstein sequence (GS) eventually reaches zero. This statement is true but unprovable in Peano arithmetic (PA). For each integer  , the Goodstein function (GF) computes the exact length of the GS associated with
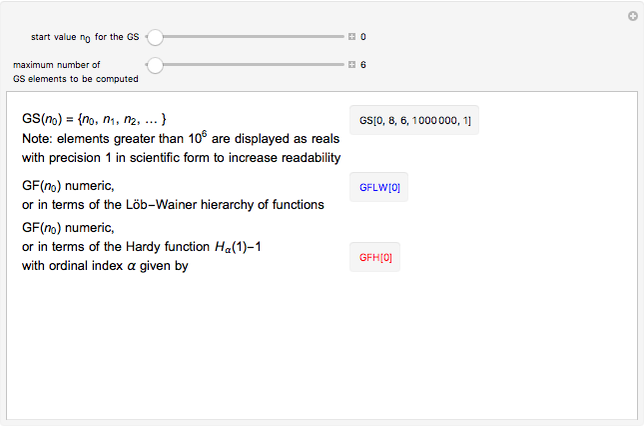
, the Goodstein function (GF) computes the exact length of the GS associated with  , that is, the number of terms needed to reach zero. The statement "GF is total" is true but unprovable in PA. In this Demonstration, the user can generate Goodstein sequences and values of the Goodstein function. For small
, that is, the number of terms needed to reach zero. The statement "GF is total" is true but unprovable in PA. In this Demonstration, the user can generate Goodstein sequences and values of the Goodstein function. For small  , GF is computed numerically; for higher
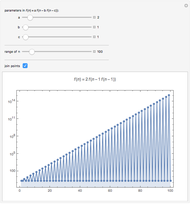
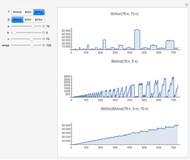
, GF is computed numerically; for higher  , GF is computed in terms of two different function hierarchies, the Löb–Wainer hierarchy and the Hardy hierarchy. Both hierarchies are fast‐growing families of functions indexed by transfinite ordinals. Hence, you can develop an idea of the explosive growth of GF well beyond the framework controlled by PA. Eventually, GF dominates every Hardy and Löb–Wainer function and is therefore not provably total in PA.
, GF is computed in terms of two different function hierarchies, the Löb–Wainer hierarchy and the Hardy hierarchy. Both hierarchies are fast‐growing families of functions indexed by transfinite ordinals. Hence, you can develop an idea of the explosive growth of GF well beyond the framework controlled by PA. Eventually, GF dominates every Hardy and Löb–Wainer function and is therefore not provably total in PA.
Contributed by: Joachim Hertel (March 2011)
Open content licensed under CC BY-NC-SA
Details
The hereditary representation of an integer 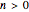 , also known as the complete base
, also known as the complete base  representation [2], represents
representation [2], represents  as a sum of powers of a base
as a sum of powers of a base  , followed by expressing each of the exponents as a sum of powers of
, followed by expressing each of the exponents as a sum of powers of  , etc., until the process stops. The change‐of‐base function
, etc., until the process stops. The change‐of‐base function  takes a natural number
takes a natural number  and changes the base
and changes the base  to
to  in the complete base
in the complete base  representation of
representation of  (see [2]).
(see [2]).
Example 1: The complete base 2 representation of 266 is 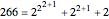 .
.
Example 2: 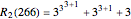 .
.
The Goodstein sequence [2,5] for  ,
, 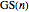 , is defined by
, is defined by 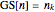 , where
, where  and
and  and
and
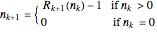 .
.
Example 3: 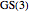 is 3,3,3,2,1,0,0,0,…
is 3,3,3,2,1,0,0,0,…
The Goodstein function [2] 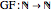 is defined as the smallest index
is defined as the smallest index  for which
for which 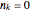 . Hence
. Hence 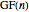 measures the effective length of
measures the effective length of  , that is,
, that is, 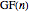 is the number of terms needed to reach 0 in the sequence
is the number of terms needed to reach 0 in the sequence 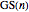 .
.
Example 4:  .
.
Now, let  denote the change-of-base function replacing each
denote the change-of-base function replacing each  by the ordinal
by the ordinal  in the complete base
in the complete base  representation of
representation of 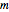 .
.
Example 5:  .
.
Chichon [1] showed that 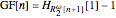 .
.
Caicedo [2] showed that for 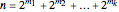 with
with 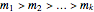 and
and  , one can write GF in terms of the Löb–Wainer functions as follows:
, one can write GF in terms of the Löb–Wainer functions as follows:
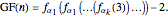
Hence GF eventually dominates every Hardy and Löb–Wainer function and therefore is not provably total in PA. Hence, the Goodstein theorem is a true but unprovable statement in PA and one of the prime examples of a natural independence phenomenon.
References
[1] E. A. Chichon, "A Short Proof of Two Recently Discovered Independence Results Using Recursion Theoretic Methods," Proc. of the AMS, 87(4), 1983 pp. 704–706.
[2] A. E. Caicedo, "Goodstein's Function," Rev. Col. de Matemáticas, 41(2), 2007 pp. 381–391.
[3] M. H. Löb and S. S. Wainer, "Hierarchies of Number Theoretic Functions I, II: A Correction," Arch. Math. Logik Grundlagenforschung 14, 1970 pp. 198–199.
[4] G. H. Hardy, "A Theorem Concerning the Infinite Cardinal Numbers," Quarterly J. of Mathematics 35, 1904.
[5] R. Goodstein, "On the Restricted Ordinal Theorem," J. of Symbolic Logic, 9(2), 1944 pp. 33–41.
Snapshots
Permanent Citation