Gram-Schmidt Process in Two Dimensions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
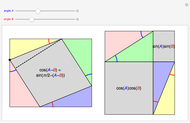
The Gram-Schmidt process is a means for converting a set of linearly independent vectors into a set of orthonormal vectors. If the set of vectors spans the ambient vector space, then this produces an orthonormal basis for the vector space.
The Gram-Schmidt process is a recursive procedure. After the first  vectors have been converted into
vectors have been converted into  orthonormal vectors, the difference between the
orthonormal vectors, the difference between the 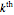 original vector and its projection onto the space spanned by the first
original vector and its projection onto the space spanned by the first  orthonormal vectors is normalized to obtain the
orthonormal vectors is normalized to obtain the 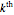 vector in the orthonormal collection.
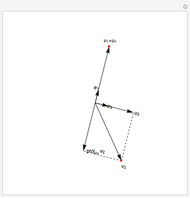
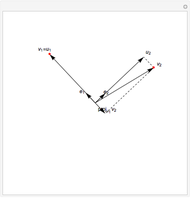
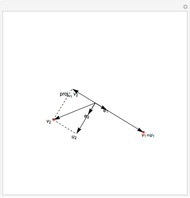
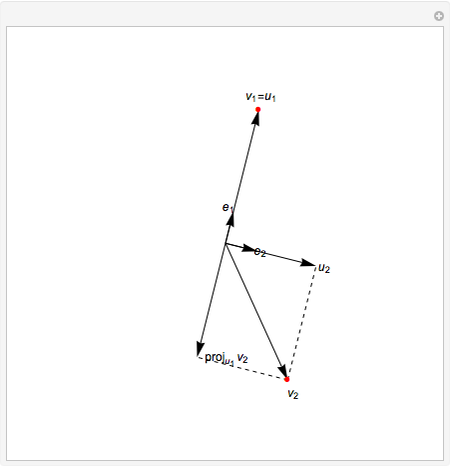
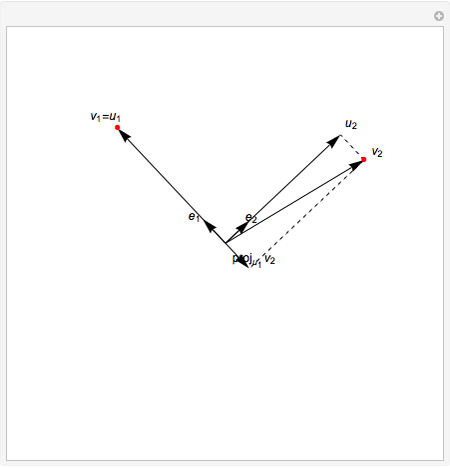
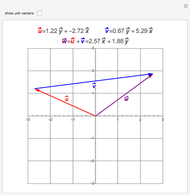
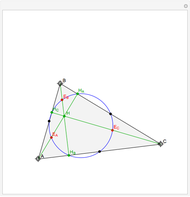
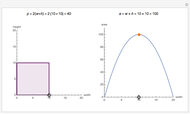
In two dimensions, start with a vector
vector in the orthonormal collection.
In two dimensions, start with a vector 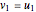 and normalize it to obtain
and normalize it to obtain 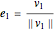 . Next, project
. Next, project 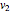 onto
onto 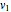 and compute
and compute 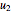 , the difference between
, the difference between  and this projection. Finally, normalize this vector to obtain
and this projection. Finally, normalize this vector to obtain 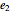 .
.
Contributed by: Chris Boucher (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Gram-Schmidt Process in Two Dimensions"
http://demonstrations.wolfram.com/GramSchmidtProcessInTwoDimensions/
Wolfram Demonstrations Project
Published: March 7 2011