Graph Searching: Breadth First and Depth First

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
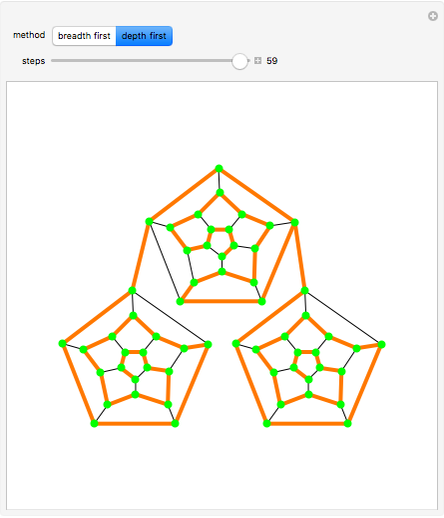
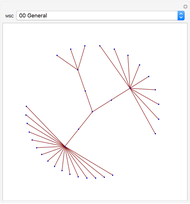
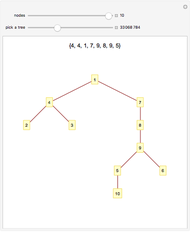
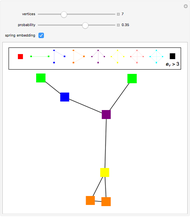
In a connected graph, you can always reach all nodes (or vertices) starting from any given node (called the root) by traversing edges. When traversing an edge from one node to another, the first is typically referred to as the "parent", and the second as the "child". Two commonly used graph traversal methods are called "breadth first" and "depth first".
Contributed by: Jeff Bryant and Daniel Lichtblau (March 2011)
Based on work by: Steven Skiena and King Larry Mak
Open content licensed under CC BY-NC-SA
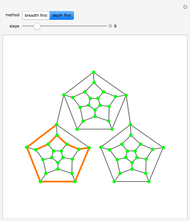
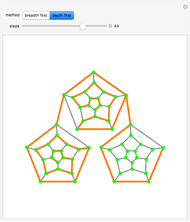
Snapshots
Details
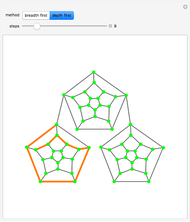
The root node is the one that is initially green. As the search encounters new nodes, they become green as well. In a breadth-first traversal, you start at the root and visit all of its children in some order. Each child is marked as having been visited. Next, a child is selected and all of its children (that is, grandchildren of the root) are visited, except those, if any, that are marked. This is repeated for the other children of the root. When that is finished, a grandchild is selected, etc. The traversal terminates when all nodes have been marked.
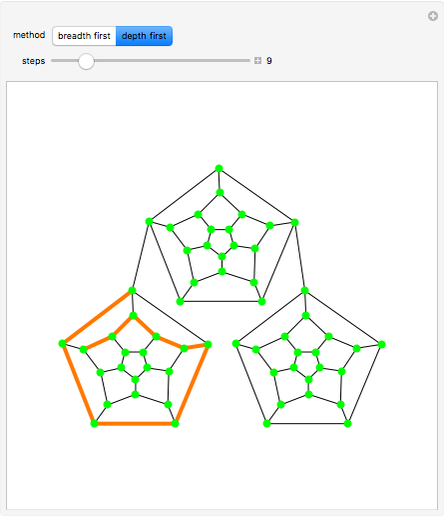
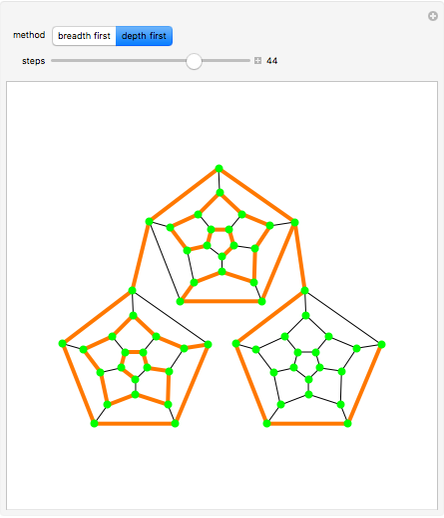
A depth-first search is done by visiting a child node (and marking it), from there selecting a grandchild, visiting and marking it, etc. Each such branch of the search concludes when there is no unmarked child to search. At that stage, you return to the parent of the last child visited, select another unvisited child, traverse to that child, and repeat. If there is no such unvisited child, you continue back up the "parent chain" until one is found with an unvisited child, whereupon you recursively visit that child in depth-first fashion.
In practice, depth-first searches are often implemented with a stack data structure. This allows the program to keep a record of children yet to be visited, in LIFO (last in, first out) order. Breadth-first searches can be accomplished using a queue structure to enforce their FIFO (first in, first out) nature.
Note that once completed, a search gives a "spanning tree", that is, a tree emanating from the root node and hitting all other nodes.
Permanent Citation
"Graph Searching: Breadth First and Depth First"
http://demonstrations.wolfram.com/GraphSearchingBreadthFirstAndDepthFirst/
Wolfram Demonstrations Project
Published: March 7 2011