Gravitational Potential of a Cuboid

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
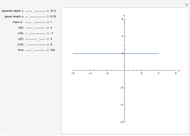
The center of mass of a cuboid with three semiaxes 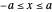 ,
, 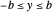 ,
, 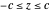 and the mass density ρ
and the mass density ρ  ) lies in the coordinate origin. The coordinates
) lies in the coordinate origin. The coordinates  ,
, 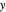 ,
,  describe the observation points running over the whole space
describe the observation points running over the whole space 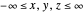 . The gravitational potential
. The gravitational potential 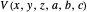 at all observation points
at all observation points  ,
,  ,
,  is a function of
is a function of 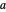 ,
,  ,
,  . The force vector
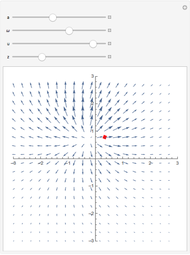
. The force vector 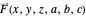 for all observation points at
for all observation points at 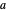 ,
,  ,
,  is computed. The potential of the cuboid at the center of the mass is
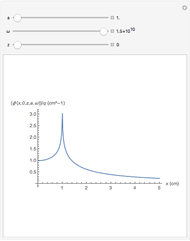
is computed. The potential of the cuboid at the center of the mass is  . The potential at the corner of the cuboid is
. The potential at the corner of the cuboid is 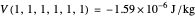 . The potential and the force vector can be computed at all observation points in and outside the cuboid. The angle between the force and the space vector is very much near
. The potential and the force vector can be computed at all observation points in and outside the cuboid. The angle between the force and the space vector is very much near  with the uncertainty of
with the uncertainty of  . The angular momentum of a particle in the gravitational field of the cuboid is time dependent and the motion is not in a two-dimensional plain near the cuboid. The potential
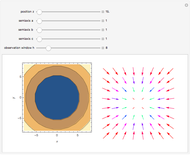
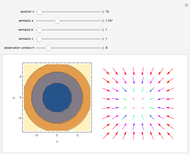
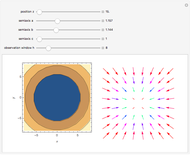
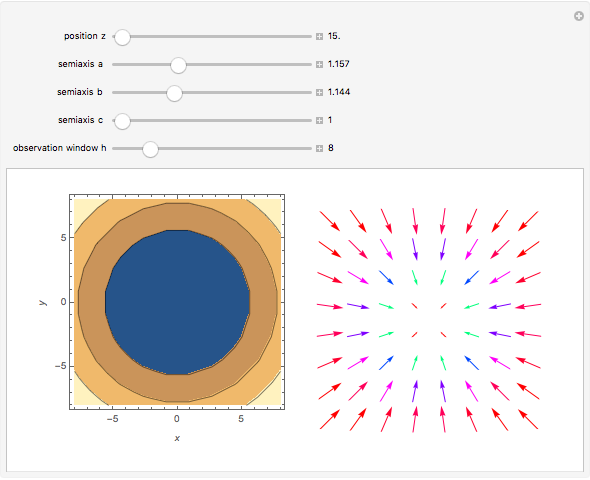
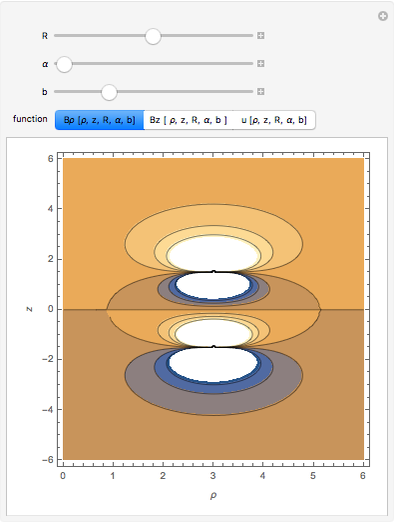
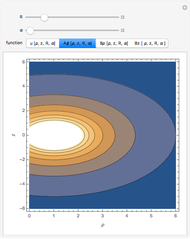
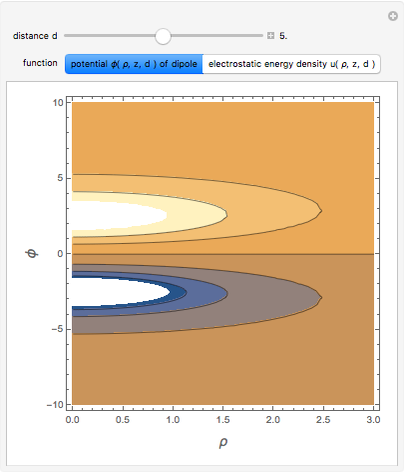
. The angular momentum of a particle in the gravitational field of the cuboid is time dependent and the motion is not in a two-dimensional plain near the cuboid. The potential  is displayed as a contour plot for the observation points
is displayed as a contour plot for the observation points 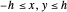 at any arbitrary
at any arbitrary  ,
, 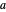 ,
,  ,
,  . The
. The 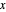 ,
, 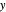 components of the force are displayed as a vector field plot.
components of the force are displayed as a vector field plot.
Contributed by: Franz Krafft (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation